직선 두개로 원을 삼등분하기
원을 삼등분하는 방법은 정말 여러가지가 있다.
일본에서는 챌린지까지 열릴정도라고하니 열기가 대단함을 알 수 있다.
그 중에는 실용적인 것도 있지만, 오로지 수학적 아름다움만을 위해 있는 것들도 있고... 하지만, 이번에 소개하려는 방식은 그 챌린지에 없지만, 실용적으로 쓸 수 있는 직선 두개로 원을 삼등분 하는 방식이다.
물론 수치가 완전히 딱 떨어지게는 나오지 않기 때문에 실전에서 사용하려면 어느정도 비슷한 근사치로 봐야하지만, 그래도 빠르게 직선만으로 3등분을 내기에는 적합하지 않나 싶다.
그래서 우리의 목표는

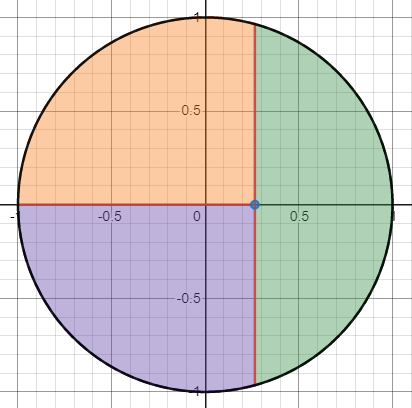
위와같이 원을 세로로 한번, 가로로 한번 잘라 면적이 동일하게 나오게 하는 것이다. 면적이 동일하면 3등분!
그렇지만, 따져보면 왼쪽의 두 부분은 위아래 대칭으로 한쪽 넓이만 계산하면 자동으로 반대편 넓이가 나오므로, 여기서 가장 중요한 포인트는 첫번째 세로로 자를 때 주황부분과 초록부분이 넓이가 같아지는지가 제일중요하게 된다.
그러면 어느 x점에서 잘라야 하는지가 중요해지고, 이것만 계산할 수 있으면 원을 직선 두개로 삼등분 할 수 있게 된다.
자, 그러면 두 넓이가 같다는 식을 세워보자

음영처리된 부분의 넓이를 구하는게 키포인트인데, 일단 간단하게 음영처리된 부분의 넓이를 $ a $라고 하고 넓이구하는 식을 만들어 봅시다. 원은 단위원으로 반지름은 1입니다.
(노란부분) $ \frac{\pi}{4} + a = 2(\frac{\pi}{4} - a) $ (초록부분)
근데 식을 써보니 식이 a에 대해서 정리될 것 같습니다.
$ \frac{\pi}{4} + a = 2(\frac{\pi}{4} - a) $
$ 3a = \frac{\pi}{4} $
$ a = \frac{\pi}{12} $
즉, 전체 넓이를 구하는 식에서 음영처리된 넓이가 $ \frac{\pi}{12} $면 된다는 식으로 식이 더 간단해 졌군요.
그럼 이제 우리는 음영처리된 넓이만 구하면 되겠습니다.
1) 각도와 삼각함수로 구하기
이전 포스팅(링크)에서 구했던 방식인데, 여기서 x값으로 다시 나타내지 않고, 각도값 그대로 사용하여 푸는 방식입니다.
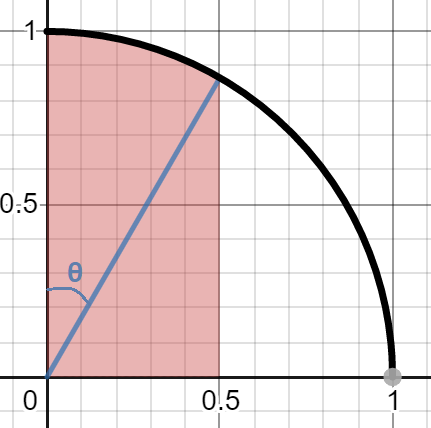
원과 각도가 주어졌고, 위와 같은 모양의 넓이면, 호의 넓이+삼각형 넓이 해서 구할수 있으며, 이 식은
$ \frac{1}{2} \theta $ (호의 넓이) + $ \frac{1}{2} sin\theta \cdot cos\theta $ (삼각형의 넓이) [r=1 생략]
그러면 우리가 구하고자 했던 $ \frac{\pi}{12} $로 방정식을 놓으면
$ \frac{1}{2} \theta + \frac{1}{2} sin\theta \cdot cos\theta = \frac{\pi}{12} $
정리하면
$ \theta + sin\theta \cdot cos\theta = \frac{\pi}{6} $
가 됩니다. 전에도 말씀드렸다시피 삼각함수의 일반각 계산은 사람이 할 수 없으므로 울프람 알파(https://www.wolframalpha.com/)를 돌려줍니다.
[위 식을 그대로 긁어서 붙이면 울프람에서 인식을 못합니다. θ + sin θ ⋅ cos θ = π/6 이거를 붙여 넣어주세요]
그러면 결과가
$ \theta = 0.268133... $
으로 나옵니다.
그러나 이거는 각도 값일 뿐, 우리가 원하는 것은 x좌표이므로, 위의 그림에서 놓은 $ \theta $ 방향을 보면, $ sin \theta $가 x좌표임을 알 수 있습니다.
다시 $ sin \theta $에 0.268133값을 넣어서 울프람 알파를 돌리면
$ sin 0.268133 = 0.264932... = x $
이와 같은 값을 얻고, 이는 바로 x좌표입니다.
2) 부정적분으로 구하기
이전 포스팅(링크)에서 주야장천 구했던 식을 가지고 푸는 방법입니다.
물론 계산은 울프람 알파가 해줄겁니다.
먼저 방정식을 세웁니다.
$ \frac{1}{2} \cdot x \cdot \sqrt{1-x^{2}} + \frac{1}{2} \cdot arcsin \, x = \frac{\pi}{12} $
정리하여
$ x \cdot \sqrt{1-x^{2}} + arcsin \, x = \frac{\pi}{6} $
으로 만들고 울프람을 돌리겠습니다. 마찬가지로 위 식을 그대로 붙이면 울프람에서 인식 못하니 x ⋅ √ (1 − x^2) + arcsin x = π/6로 붙여넣어 주세요.
그러면 이번에는 한번에 x 값을 알려줍니다. 결과는 1)번과 같습니다.
결론
위의 계산으로 단위원의 원점에서 약 0.265만큼 떨어진 위치에서 세로로 한번, 나머지 부분에 가로로 한번 잘라주면 3등분이 된다는 사실을 알았네요!
좀 더 실용적으로 말해보자면 어떤 크기의 원이든, 원점에서 약 1/4 지점보다 조금 더 나가서 T자로 자르면 3분할이 된다고 볼 수 있겠습니다!
'Study > Mathematics' 카테고리의 다른 글
| 멱급수 전개(Power series expansion)로 피보나치 수열 풀기 (0) | 2024.06.30 |
|---|---|
| 점화식에서의 특성방정식(characteristic equation) (87) | 2024.01.25 |
| 원넓이의 부정적분 구하기 - 2) 부정적분으로 구해보기 (0) | 2020.10.23 |
| 원넓이의 부정적분 구하기 - 1) 일반공식으로 구해보기 (0) | 2020.07.23 |
| 피보나치 수열의 일반항과 비율의 극한(황금비) (2) | 2020.05.04 |