카탈란 수열의 점화식 구하기

카탈란 수열의 점화식 구하기

 
0. 서론

저번 포스팅까지 해서 카탈란 수열의 일반항을 아주 직관적으로 조합적 방식을 통하여 구해보았습니다.
사실 개인적으로는 이거보다 더 깔끔하게 설명할 수 있나!? 싶을 정도로 자화자찬하고 싶습니다만...
오늘은 카탈란 수열의 점화식에 대해서 살펴보겠습니다.

 
1. 카탈란 수열의 점화식?

사실상 '카탈란 수열에도 점화식이 있어!?'라는 질문이 처음 나오는게 너무나도 당연한 시작일 것이라고 생각합니다.
왜냐면 사실 카탈란 수(카탈랑 수) 라는 거 자체가 처음부터 수열을 만들기 위한 정의 자체가 아니었거든요.

원래는 '문제풀이'가 카탈란 수의 본질이라면 본질이라고 볼 수 있습니다.

첫 포스팅에서 알아볼때, 참 많은 문제들의 답안으로 카탈란 수열이 사용된다고 알아보았습니다.
다시 정리하자면 가장 독특한게 괄호치기 문제, 그리고 그 다음으로 볼록 n+2각형에서 n개의 삼각형으로 분할하는 경우의 수, 뒤크 경로(Dyck path) 풀이(딕 경로라고도 부르는데요, 카탈란 수열 구하면서 봤죠? 엄밀하게는 격자이동 없이 우상향, 우하향하는 경로를 Dyck path라고 합니다), 뒤크 문자열의 수, 원 위에 2n개 점 잡고 n개 선분 그릴때 교점 없이 긋는 방법의 수, n개의 노드를 가지는 이진트리 구성 방법의 수, 스택정렬 가능한 경우의 수 등 여러 조합론적 문제에서 답이 되는 수 입니다.
그리고 그만큼 '어떤 n에 대해서 어떤 경우의 수를 가지나~'하는게 카탈랑 수의 본질이죠.

그래서 사실 점화식도 이후에 유도된 것이라고 봐도 무방합니다.(애초에 점화식으로 정의된 수열이 아니걸랑요!)

따라서 애초에 점화식으로 정의되며, 수열을 기본적으로 정의로 가지는 피보나치 수열과는 차이가 있습니다.
그럼에도 불구하고 이 카탈란 수를 이용한 수열은 어떠한 규칙성을 가지고 수를 계속 만들어 내기 때문에 수열이라고 볼 수 있는거구요.

 

2. 점화식은 어떻게 구할까?

사실 위에서 수많은 예시를 들었고, 그 예시들을 가지고 문제를 풀다보면 점화식은 쉽게 도출됩니다.
오히려 점화식에 비해 일반항이 구하기 어려운 편인데, 그마저도 격자이동에서의 Dyck path를 구하는 문제로 보면 쉽게 구할 수 있죠.(그래서 이걸로 카탈란 수의 일반항을 먼저 구했었죠)
(점화식으로 쉽게 정의되어 만들어진 피보나치 수열이 오히려 일반항은 굉장히 어렵게 구해지던 거랑 정 반대죠?)

그럼 저런 수많은 예시들을 놓고 어떤 방법으로 구해야 가장 쉽게 구해질까!? 하면, 사실 괄호치기 문제가 제일 간단하게 구할 수 있습니다.
물론, Dyck path문제로도 구할 수 있는데 이거는 아주 약간의 기하학적 아이디어들이 들어가야하므로 먼저 괄호치기 문제로 귀납적으로 점화식을 구하고, 그 다음 구해보도록 하겠습니다.(심지어 기하학적 아이디어 없이 수열분해부터 들어가면 어렵습니다)

 

3. 카탈란 수열의 점화식을 구해보자

 

3-1. 괄호치기 문제

괄호치기 문제로 점화식을 구하는게 왜 쉬운지는, 이후에 Dyck path를 통해 구하면서 알아보기로 하고 일단 구해봅시다.

- 괄호가 아예없다면 보나마나 경우의 수는 1입니다. = $ C_0 $

- 괄호가 '(' 하나 ')' 하나 있다면 경우의 수는 1입니다 = $ C_1 $

- 괄호가 '(' 두개 ')' 두개 있다면 경우의 수는 2입니다 = $ C_2 $
    ()(), (()) 이렇게 되겠지요?
    여기서 첫 괄호가 열리고 닫히는걸 주목해 봅시다.
    첫 괄호가 열리고 나서 어쩌구 저쩌구 한 뒤에 닫힌 경우와 그 뒤의 경우를 나눠서 생각해보면
    * ()() 경우에는
        첫 괄호가 열린 뒤 아무것도 하지 않고 닫혔고, 그 뒤에는 괄호가 한번 열리고 닫혔습니다.
        첫 괄호가 열린 뒤 아무 것도 하지 않고 닫혔다 = $ C_0 $
        그리고 그 뒤에 괄호가 한번 열리고 닫혔다 = $ C_1 $
        동시에 일어났으니까 곱하기!
        결국 $ C_0 \cdot C_1 $
    * (()) 경우에는
        첫 괄호가 열린 뒤 괄호가 한번 열리고 닫히고나서 첫 괄호가 닫혔고, 그 이후에는 뭐 어떻게 할 괄호가 없네요.
        첫 괄호가 열린 뒤 괄호가 한번 열리고 닫히고 나서 첫 괄호가 닫혔다 = $ C_1 $
        이후에는 괄호가 없다 = $ C_0 $
        곱해서 나타내면 $ C_1 \cdot C_0 $
    그리고 이 두가지 경우를 더해서 경우의 수를 나타내면 $ C_0 \cdot C_1 + C_1 \cdot C_0 $
    결과는 2입니다!

여기서 왜 첫괄호가 열리고 닫히는건 신경도 안쓰냐! 하실 수 있는데, 카탈란 수의 구조에서 ‘( )’처럼 괄호를 열자마자 바로 닫는 경우는, 구조적으로 아무것도 하지 않고 본래 상태로 되돌아온 것과 같습니다.
점화식에서는 첫 괄호쌍이 닫히는 시점(즉, 원점으로 돌아온 시점)을 기준으로 경로를 나누기 때문에(첫 원점이 제일 중요합니다. 첫 원점 이후 상황은 카탈란 수로 바로 결정되거든요), ‘열자마자 닫는’ 경우는 앞부분에서 유의미한 구조를 형성하지 못하므로, 기저적으로 $ C_0 (=1) $에 해당하는, 의미 없는 기본 단위로 간주하는 것입니다.
좀 더 그럴듯한 이유는 이어지는 Dyck path 문제에서 한번 더 살펴보시죠!

- 이젠 각 괄호가 세개씩 있는 상황입니다.
()()()
()(())
(())()
(()())
((()))
자, 첫 괄호가 닫히는 시점이 중요하다고 했죠?
잘 보면 첫 괄호가 닫히는 시점이 세가지로 나뉘는 걸 알 수 있습니다.
첫괄호가 바로 닫히는 경우
첫 괄호안에 괄호가 하나 있는경우
첫 괄호안에 괄호가 두개 있는경우
이렇게 말이죠.
첫 괄호가 열리자마자 닫히면 구조적으로 $ C_0 $ 라고 하였습니다.
그리고 그 뒤를 보면 바로 위에서 했던 모양이 보이죠? $ C_2 $입니다.
첫 괄호가 바로 닫히는 경우 클리어했습니다.
그 다음 첫 괄호 안에 괄호가 하나 있는 경우를 보겠습니다.
첫 괄호 안에 괄호 하나는 $ C_1 $이겠군요? 그리고 그 뒤로 괄호 하나가 더 나오니 또 $ C_1 $입니다. 두번째 조건도 클리어!
첫 괄호 안에 괄호가 두개 있는 조건도 보겠습니다.
첫 괄호 안에 괄호가 두개니까(그리고 그 모양은 바로 위에서 살펴보았던 모양) $ C_2 $겠군요.
그리고 그 뒤에는 남은 괄호가 없으니 $ C_0 $겠어요..
그러면 결국 다 더하면 $ C_3 = C_0C_2 + C_1C_1 + C_2C_0 $ 겠네요! 값은 5구요!

그리고 여기서 '점화식'이라고 볼 수 있는 것이 나옵니다.

눈치 빠르시면 아시겠지만, 바로 이전까지 나왔던 카탈란 수가 다음 카탈란 수를 결정하고 있는게 보이시나요?

그리고 규칙성도 보이지 않습니까?

그럼 지금까지 살펴본 것을 바탕으로 귀납적으로 사고해봅시다.

 

만약 $ C_n $의 점화식을 본다면,

1) 첫 괄호가 닫히는 걸 기준으로, '앞 카탈란 수'와 '뒷 카탈란 수'의 곱을 구분한다고 볼 수 있으므로 항은 n개가 생성이 될겁니다.

2) '앞 카탈란 수'는 첫 괄호 내에 계속해서 괄호들이 한 쌍씩 추가 될 것이므로 $ C_0 $부터 $ C_{n-1} $까지 늘어나겠네요(첫 괄호에서 이미 한쌍을 사용하죠? 그래서 n-1까지만 늘어납니다.)

3) '뒷 카탈란 수'는 남는 괄호를 가지고 만들어지는 카탈란 수니까 첫 괄호에 한쌍을 사용하고 남는 괄호들로 만들어지므로 $ C_{n-1} $부터 $ C_0 $까지 줄어들겠네요!

수식으로 써보면

$ C_n = C_0 C_{n-1} + C_1C_{n-2} + \cdots + C_{n-2} C_1 + C_{n-1} C_0 $

가 되겠구요!

 

$ C_4 $로 한번 확인해볼까요?

$ C_4 = C_0 C_3 + C_1 C_2 + C_2 C_1 + C_3 C_0 $

카탈란수가 0항부터 3항까지 각각 1, 1, 2, 5의 값을 가지니까, 계산해보면

$ C_4 = 1*5 + 1*2 + 2*1 + 5*1 = 14 $

예, 정답이 나오네요! 점화식을 귀납적으로 잘 찾아낸 것 같습니다!

 

근데, 저렇게 덧셈을 주루룩 늘어놓으면 보기가 별로 좋지 않죠...?

그래서 우리는 summation으로 저것을 간단하게 표현해 볼 것입니다. 대문자 sigma죠!

규칙도 간단합니다. 0부터 n-1까지 커지는거 하나, n-1에서 0까지 작아지는거 하나!

$ C_n = \sum\limits_{k=0}^{n-1} C_k C_{n-1-k} $

이렇게 간단(?)하고 깔끔(?)하게 카탈란 수열의 점화식을 구해보았습니다!

 

사실, 곰곰이 생각해보면 맞는 말이긴 하지만, 그럼에도 귀납법으로 유추를 하기도 하고 왠지 설명이 조금 부족하다 싶은 부분이 있을 수도 있습니다.

그럼 이어서 Dyck path로 구하는 법을 보도록 하죠.

 

3-2. Dyck path 문제

이번에는 Dyck path의 구조적 성질을 활용해 연역적으로 점화식을 유도해보겠습니다.

기하학적으로 보면 제일 깔끔한 유도방식이 아닐까 싶네요.

그러나 여기서는 각 점별로 하나하나 생각해 주는 것도 필요하고, 더군다나 prime Dyck path, 최초 귀환 이라는 개념들이 새로 나오는게 문제지만요, 사실 뭐 별다른 개념도 아닙니다.

자, 일단 개념 들어갑시다!

1] 최초 귀환점

'최초 귀환점'이란건, (0,0)에서 출발해서 Dyck path를 따라가다가 제일 처음으로 y=x선이랑 만나는 지점을 '최초 귀환점'이라고 합니다.

R과 U가 짝이 맞으면 다시 처음부터 이동하는 것과 마찬가지라고 생각할 수 있으므로 '다시 돌아왔다'고 볼 수 있는데, 직감적으로 이해가 되시죠?[혹은 0에서 출발해서 R이 +1, U가 -1이라고 보면 R하고 U가 짝이 맞으면(+1 + (-1)) 다시 0이 되죠?]

 

출발점 (0,0)은 귀환점에 포함되지 않으며, 일반적으로 (1,1), (2,2), ..., (n,n)까지 n개의 귀환점이 생깁니다.

이 최초 귀환점을 기준으로 경로를 두 부분으로 분해할 수 있습니다:

• 최초 귀환점까지의 경로 (앞 구간)
• 그 이후부터 종점까지의 경로 (뒷 구간)

 

n=2인 격자에서 그림으로 보자면, (1, 1)과 (2, 2)가 최초귀환점이 됩니다.

 

2] prime Dyck path

prime이라는 단어는 '더이상 분해할 수 없는' 상황에 붙이는 단어인데(1과 자기자신 이외에는 나눠지지 않는 수가 소수(prime number)죠) 이를 통해 유추해보자면 'Dyck path 중 더이상 분해되지 않는 Dyck path다'라고 생각해 볼 수 있습니다.

이게 무슨말인고?하니.. n=2인 격자를 한번 생각해보죠.[바로 위에 이미지가 있죠?]

Dyck path는 두 가지가 있는데, 하나는 중간에 y=x선에 닿았다가 진행하는 경우이고, 하나는 닿지 않고 진행하는 경우입니다.

여기서 잘 생각해보면, y=x선에 닿은 Dyck path(왼쪽)는 y=x선에 닿은 점을 기준으로 앞쪽 Dyck path랑 뒤쪽 Dyck path로 분해할 수 있게 되겠죠?

그런데, 두번째인 오른쪽의 경우는 그냥 그 자체로 하나의 Dyck path이지, 다른 Dyck path들로 분해할 수 없죠?

그래서 바로 오른쪽과 같은 경로를 prime Dyck path라고 부릅니다.

결국 prime Dyck path란 처음 출발 이후 종점에 도착할 때까지 한번도 y=x선에 닿지 않으면서 이동하는 경로를 말하는 것이죠.

 

3] prime Dyck path의 개수 구하기

저번 포스팅의 기억을 한번 돌이켜 볼까요?

저번 포스팅에서 Dyck path의 경우의 수는 전체 경로에서 Dyck path를 위반한 경로를 빼서 구했었습니다.

그때 Dyck path를 위반한 경로는 어떻게 구했나요?

'y=x선을 넘어간 애는 위반한 애야 $ \leftrightarrow $ y=x+1선과 닿은 애는 위반한 애야'

라고, 새로운 선을 하나 추가해서 풀었었죠!

 

그럼 이 아이디어를 다시 차용해 봅시다.

 

prime Dyck path는 y=x 선에 닿지 않아야 합니다.(위에서 살펴봤듯이 닿으면, 그 점을 기준으로 분해가 된다고 했죠?)

그렇다면, y=x-1 아래에서만 움직이는 경로는 그 어떤 상황에서도 절대로 y=x선과 닿을 수 없겠죠?

그리고 y=x-1 아래에서만 움직이기 위해서는 처음 y=x-1 선 아래로 움직이는 R 한번, 그리고 y=x-1 선에서 종점으로 움직이는 U 한번이 필수적으로 필요하다고 볼 수 있겠습니다.

 

따라서 n x n 격자에서 prime Dyck path의 수는 (n-1) x (n-1)을 움직이는 Dyck path의 수와 같아집니다.

 

2 x 2 격자에서 prime Dyck path의 수는 1 x 1 Dyck path의 수 즉, $ C_1 = 1 $입니다.

3 x 3 격자에서 prime Dyck path의 수는 2 x 2 Dyck path의 수 즉, $ C_2 = 2 $입니다.

4 x 4 격자에서 prime Dyck path의 수는 3 x 3 Dyck path의 수 즉, $ C_3 = 5 $입니다.

 

4] 그렇다면 1 x 1 격자에서 prime Dyck path의 수는 어떻게 될까요?

여기서 위에서 살펴보았던 괄호치기에서 왜 맨처음 열고닫는 괄호는 생각하지 않는지에 대한 해답이 있습니다.

 

1>> 지금까지 구한 대로라면 0 x 0 Dyck path의 수 즉, $ C_0 = 1 $이어야 합니다.(그리고 이 결과는 썩 괜찮은 논리적 귀결입니다.)

그러나 아직까지도 우리는 'R한번 U한번으로 움직이는 경로가 있잖아! 얘는 prime Dyck path아냐? 분해불가잖아!'라고 생각할 수 있습니다.

 2>> 하지만 생각해보면 prime Dyck path란건 시점과 종점을 제외하고 중간에 한번은 닿을 수 있는 점이 있을 때만(= 분해 가능한 경우가 있어야만) 정의가 됩니다.

어떻게 요렇게 조렇게 조합하면 분해할 수 있는 상황에서, 특별한 방법의 조합으로 분해가 불가능한 상황을 정의한 거니까요.

[가령 RURU는 분해가능한 조합이고, 이걸 특별한 방법으로 RRUU로 조합하면 분해가 불가능한 prime Dyck path가 되죠]

그렇다면 너무나도 당연하게 시점과 종점만 있는 상황에서는 prime Dyck path를 정의할 수 없습니다.

[또 다르게 생각해서 1이 소수(prime number)가 아닌 이유와도 상통하겠네요, 1x1에서는 prime Dyck path가 없습니다.]

3>> 다르게 생각하면 하나 작은 격자의 Dyck path를 구함에 있어 그 하나 작은 격자로 '들어가는' 한 스텝과, '나오는' 한 스텝은 필수적으로 필요하기 때문에 카운트 안한다고 생각하셔도 무방합니다.

 

자, 이제 괄호치기 문제에서 왜 첫번째 괄호를 열고 닫는건 카운트하지 않는지에 대해서 아주 명확하게 해결이 되었습니다.

괄호치기 문제에서의 설명에 더불어 1, 2, 3번 설명 중 와닿는 설명으로 이해하시면 됩니다.

 

어찌됐든 그래서 첫 카탈란 조합(RU던 ()던)은 노카운트($ C_0 $)입니다!

 

5] 격자에서의 Dyck path 문제 규칙 살펴보기

요지는 간단합니다.

n x n 격자에서 Dyck path의 경우의 수는 최초 귀환점들로 분해할 수 있습니다.(물론 분해된 모든 경로는 Dyck path일테니 카탈란 규칙을 만족한다는 가정입니다)

따라서 너무나 당연하게도 최초 귀환점들로 분해해서 구한 Dyck path들을 다시 다 더하면 전체 Dyck path의 경우의 수가 될 것입니다.

그리고 최초 귀환점을 기준으로, 최초 귀환점 앞부분은 무조건 prime Dyck path여야 하고(당연히 '최초'귀환이니 y=x에 닿는 지점이 없어야 겠죠?)

그 뒷부분은 그냥 Dyck path이기만 하면 됩니다. 그리고 이 Dyck path를 가지는 경우의 수가 바로 카탈란 수였죠?

그리고 더불어 이렇게 분해를 함으로써 항상 이 분해된 Dyck path의 경우의 수는 전체 경우의 수보다 작아지게 됩니다.

결국 '이전의 수들로 다음 수를 결정한다'는 점화식의 정의를 만족하게 되고, 이 방법론을 따라가면 카탈란 수열의 점화식을 알 수 있게 되겠네요!

 

바로 n이니 k니 문자를 사용해서 유도를 하면 복잡하고 와닿지도 않게되니, 일단 n=3인 상황을 봅시다.(n=2는 위에서 살펴보았죠?)

아까 prime Dyck path는 y=x-1을 넘지않는 Dyck path의 수라고 했습니다.

그리고 이 말은 항상 최초귀환 점보다 1작은 격자를 Dyck path를 따라 움직이는 것과 마찬가지인 경우의 수를 가지게 됩니다.

이미지로 살펴볼까요?

최초귀환점이 (1, 1)인 경우를 보면 다음과 같습니다.

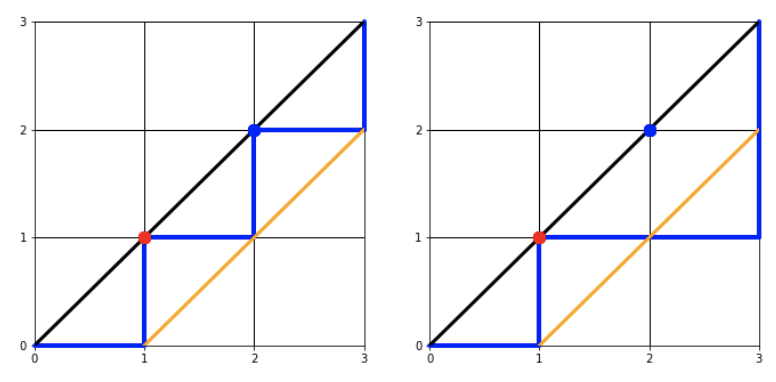
보시면 아시겠지만, y=x-1선(오렌지색) 아래로 움직일 수 있는 방법이 전혀 없습니다.

이번엔 최초귀환점이 (2, 2)인 경우를 볼까요?

잘 보면 y=x-1보다 아래 즉, (2, 2)보다 1작은 1x1격자(빨간색)에서 Dyck path를 만족하는 경로를 움직이는 것이 prime Dyck path임이 보입니다.

 

이번엔 마지막 (3, 3)이 최초귀환인 상황을 보죠.

마찬가지로 y=x-1보다 아래 즉, 1작은 (2, 2)격자를 Dyck path로 움직이는 경로가 (3, 3)에서의 prime Dyck path가 됨을 알 수 있습니다.

 

6] Dyck path 문제로 점화식 구하기

이로써 모든 규칙을 파악했습니다.

 

1. 격자이동문제에서 Dyck path는 (0, 0)에서 (2n, 0)까지 도달하는 경로 중, y=x선 위로 올라가지 않는 경로이다. 이러한 경로는 (0, 0)을 출발하여 항상 최초로 y=x선에 다시 닿는 지점을 기준으로 두 부분으로 분해할 수 있다.[앞구간, 뒷구간] 그리고 이 다시 닿는 지점을 최초귀환점이라 한다.

 

2. 최초귀환점은 R과 U가 같은 상황에서 빌생하므로 (1, 1)부터 (n, n)까지 항상 n개가 발생한다.

 

3. 이 최초귀환점은 항상 (k, k)의 형태이며, 최초귀환점 이전 구간(앞 구간)은 항상 y=x-1선을 넘지않는 prime Dyck path가 된다. 이 부분은 본질적으로 $ C_{k-1} $개의 경우의 수를 가진다.

 

4. 최초귀환 이후의 경로는 (k, k)에서 시작하여 (2n, 0)까지 도달하는 일반적인 Dyck path이므로, 이는 $ C_{n-k} $개의 경우의 수를 가진다.

 

5. 따라서 $ C_n $은 가능한 모든 최초귀환점 k(k=1~n)에 대해 $ C_{k-1} \cdot C_{n-k} $의 합으로 표현할 수 있다.

 

6. 이에 따라 점화식이 유도된다:

$ C_n = \sum \limits _{k=1}^{n} C_{k-1} \cdot C_{n-k} \quad (C_0=1, \  n \ge 1) $

$ \Leftrightarrow C_n = \sum \limits _{k=0}^{n-1} C_k \cdot C_{n-(k+1)} \Leftrightarrow C_n = \sum \limits _{k=0}^{n-1} C_k \cdot C_{n-k-1} \quad (C_0=1, \  n \ge 1) \ \blacksquare $

[아랫식으로의 변형은 식에서 k를 1씩 더하고 summation의 범위를 1씩 빼서 동치로 만든 것이다.

그러나 우리가 유도한 것과 다르게 처음에 U와 R을 한개씩 쓴 것으로 생각하고 index를 유도하면 다음과 같은 해석도 가능하다.

- 앞 부분은 k쌍 중 1쌍을 뺀, 즉 2(k−1)짜리 Dyck path 수 → $C_{k-1}$  
- 뒷 부분은 전체 n쌍 중 첫 1쌍을 뺀 (n−1)쌍에서 다시 k쌍을 뺀 Dyck path 수 → $C_{n-1-k}$
이러한 해석을 통해 바로 아랫식으로의 유도도 자연스럽게 가능하다. 그러나 어떻게 해석하든 결과는 같다.]

 

이것으로 격자이동에서의 Dyck path의 구조적 성질에 의거한 연역법(structural deduction)으로 카탈란수의 점화식을 구했습니다.

연역법으로 구하였기에 보편타당한 식이 유도되었으며, 이를통해 귀납적으로 구한 점화식도 맞다는 것이 입증되었네요!

 

 

4. 마무리

카탈란 수열의 점화식

$ C_n = \sum \limits _{k=0}^{n-1} C_k \cdot C_{n-1-k} \quad (C_0 = 1, \  n \ge 1) $

 

 

오늘은 여러가지 방법을 통해 카탈란 수열의 점화식을 유도해 보았습니다.

 

다음에는 이를 응용하여, n+2각형에서 n개의 삼각형으로 분할하는 경우의 수에 대해 알아보도록하겠습니다!