직선 두개로 뢸로 삼각형(Reuleaux triangle) 4등분 하기
[바라크루드(Baraclude) 4등분(4분할)하기]
말머리-
여러분은 뢸로 삼각형(Reuleaux triangle)이라는 걸 아시나요?
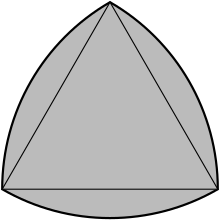
요렇게 생긴 삼각형이랍니다.
정삼각형의 각 꼭지점에서 그 변을 반지름으로하는 호를 그렸을 때 만들어지는 도형이죠!
그리고 이 도형의 특징은! 바로 등폭도형(curve of constant width)이라는거죠!
그 뜻은 이 도형의 어느 양 끝을 기준으로 삼아도 폭이 일정하다는 말입니다.(그도그럴게 정삼각형의 한 변을 기준으로 각각 호를 그렸으니 너무나도 당연한 결과죠!)
그리고 여기서 폭은 정삼각형의 한 변의 길이가 됩니다.
그러나 오늘은 이 뢸로 삼각형을 소개하는 것 뿐만이 아니라, 이 뢸로삼각형을 같은 넓이로 4등분해 볼건데요!
왜 요런짓을 하는지는 나중에 마무리부분에서 보기로 하고 일단 4등분 고고싱 해보죠
고고싱~
수식세우기-
1] 전체 넓이 구하기
일단 4등분을 하려면 과거 >>직선 두개로 원 삼등분하기<<처럼 전체 넓이를 기준으로 계산을 하는 것이 편합니다.
따라서 이 뢸로 삼각형의 전체 넓이 S를 구해보겠습니다.
언뜻 '아니 곡선으로 이루어진 도형의 넓이를 어떻게 구해?' 싶지만, 의외로 부채꼴의 조합이므로 계산이 어렵지 않아요!
[전체넓이 = 한 부채꼴의 넓이*3 - 삼각형의 넓이*2] 로 구할 수 있답니다!
여기서 부채꼴의 반지름 r은 등폭도형이므로 폭 d와 같습니다.(폭 d는 정삼각형 한 변의 길이와도 같죠)
또한 부채꼴의 각도는 60도이므로(정삼각형의 한 각과 같습니다) 라디안으로 쓰면 $ \frac{\pi}{3} $죠
한 부채꼴의 넓이: $ \frac{1}{2}r^2\theta = \frac{1}{2}d^2\frac{\pi}{3} $
정삼각형의 넓이: $ \frac{\sqrt{3}}{4}d^2 $
그렇다면 부채꼴 넓이 *3-정삼각형 넓이는
$ S = \frac{1}{2}d^2\frac{\pi}{3}*3 - \frac{\sqrt{3}}{4}d^2*2 $
$ S = \frac{1}{2}d^2(\pi - \sqrt{3}) $
자, 그러면 이 전체넓이의 $ \frac{1}{4} $을 부분넓이 구하는 식에서 찾으면 되겠죠?
$ \frac{S}{4} = \frac{1}{8}d^2(\pi - \sqrt{3}) $
2] 부분넓이 구하기
자, 이제 '어느 높이에서 이 뢸로 삼각형의 넓이는 이만큼입니다~'하고 알려주는 부분넓이 공식이 필요한데... 아무래도 호(arc)이다 보니 계산이 녹록치 않아보이죠?
일단 계산이 쉽게 좌표 세팅부터 해주겠습니다.
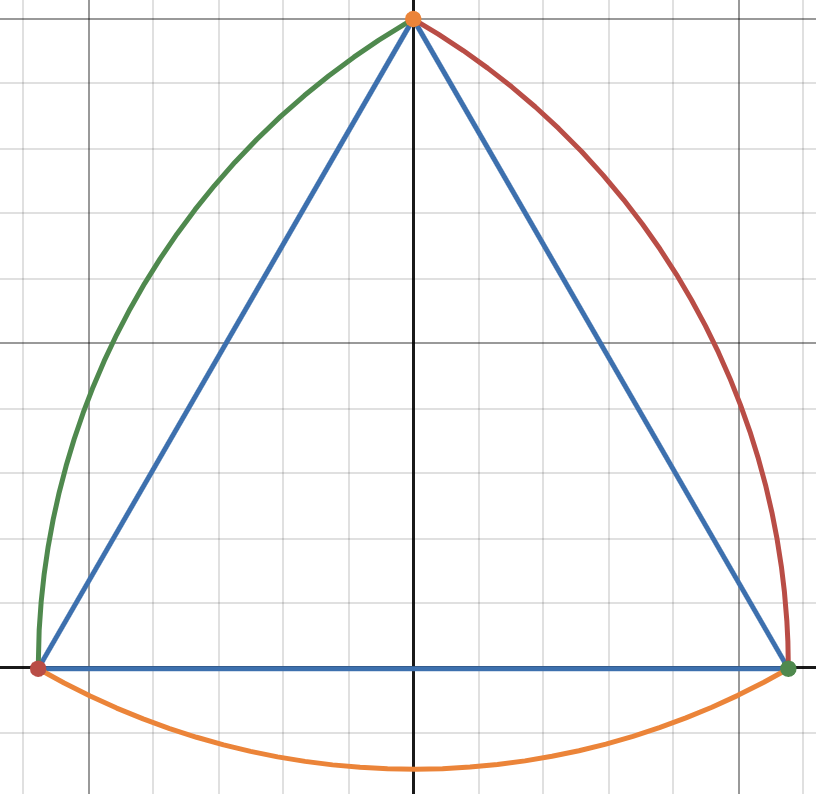
자, 먼저 정삼각형의 밑변을 x축에 접하게두고, y축의 중심에 놓습니다.
이렇게두면 정삼각형은 y축으로 이등분이 되는 꼴이 되겠죠, 그리고 좌우 대칭일 겁니다
이걸로 일단 4등분을 할 때 세로로 2등분은 해결이 되었습니다. 무조건 세로로 2등분하면 넓이는 절반이 되겠죠
그렇다면 가로로 2등분 점을 찾아야 한다는 결과에 도달합니다.
그러면 세로로 2등분, 가로로 어느정도 높이에서 2등분하면 전체 넓이의 $ \frac{1}{4} $이 되는 넓이가 나올겁니다. 이 높이를 찾으면 되겠네요.
폭이 d라고 했으니, 오른쪽 빨간색 호의 중심은 왼쪽아래 빨간점이 되겠고 좌표는 ($-\frac{d}{2}$, 0)
그러면 이 부채꼴의 원래 원의 방정식은
$ (x + \frac{d}{2})^2+y^2=d^2 $이 될겁니다.
그럼 이 식을 정리해서, x좌표에 대한 식으로 변형한 다음 0부터 어떤 지점 a까지 적분하면 이 뢸로삼각형의 부채꼴의 일부의 넓이를 구할 수 있겠네요! 이 넓이를 T라고 해보죠(a부터 $ \frac{\sqrt{3}}{2}d $까지 구할 수도 있으나, 밑끝이나 위끝에 0이 들어가야 적분식이 깔끔해지는 경향이 있어 그냥 0부터 적분하겠습니다.)
자, 근데 하나 문제가 있죠. 이거는 0부터 적분해가는 식인데, 저희가 놓은 좌표대로면 아래쪽 활꼴(주황색)의 넓이가 반영이 안됩니다.
근데, 뭐 이 활꼴의 넓이는 너무 쉬우니까 바로 계산해보죠
활꼴의 넓이 = 부채꼴의 넓이-삼각형의 넓이
$ A_{sector} = \frac{1}{2}d^2\frac{\pi}{3} $
$ A_{triangle} = \frac{\sqrt{3}}{4}d^2 $
$ A_{segment} = \frac{1}{2}d^2\frac{\pi}{3} -\frac{\sqrt{3}}{4}d^2 $
$ A_{segment} = \frac{1}{2}d^2(\frac{\pi}{3} -\frac{\sqrt{3}}{2}) $
근데 여기서 절반의 넓이만 포함되어야하므로
$ \frac{1}{2}A_{segment} = \frac{1}{4}d^2(\frac{\pi}{3} -\frac{\sqrt{3}}{2}) $
그러면
$ \frac{1}{4}S = \frac{1}{2}A_{segment} + T$(0부터 a까지 부채꼴의 일부의 넓이 적분)
이면 높이 a를 구할 수 있겠군요!
영역으로 보자면, 오른쪽 위에 해당하는 1사분면만 적분이 되어야 하구요
일단 찾은 원의 방정식을 정리해봅시다.
$ (x + \frac{d}{2})^2+y^2=d^2 $
$ (x + \frac{d}{2})^2=d^2-y^2 $
$ x + \frac{d}{2}=\pm \sqrt{d^2-y^2} $
$ x=\sqrt{d^2-y^2} - \frac{d}{2} $
로 정리가 되었습니다.
여기서 마지막줄로 정리할 때 제곱근의 양수만 취한 것은 오른쪽 영역만 표현하는 함수를 얻기 위함이며, y값이 음수와 양수를 모두 포함하더라도 적분 자체에서 0부터 a까지 적분할 예정이므로 y값의 영역이 정해지기에 문제가 없습니다!
그러면 적분을 해봅시다
$ T = \int_{0}^{a} (\sqrt{d^2-y^2} - \frac{d}{2}) dy $
$ T = \int_{0}^{a} \sqrt{d^2-y^2} dy - \int_0^a \frac{d}{2} dy $
$ T = \int_{0}^{a} \sqrt{d^2-y^2} dy - [\frac{d}{2}y]^a_0 $
$ T = \int_{0}^{a} \sqrt{d^2-y^2} dy - \frac{d}{2}a $
자, 적분의 뒤쪽영역은 아주 쉽게 적분이 되었으나, 앞쪽은 쉽지 않아보이네요?
원을 적분할 때 가장 많이 쓰이는 트릭이 치환 적분에서 y를 r * sin t로 놓는 것입니다. 똑같이 적용해보죠
$ y = d*sin\theta $
$ dy = d*cos\theta d\theta $
$ T_1 = \int_{0}^{a} \sqrt{d^2-(d*sin\theta)^2} * d*cos\theta d\theta $
$ T_1 = \int_{0}^{a} d*\sqrt{1-(sin\theta)^2} * d*cos\theta d\theta $
$ T_1 = \int_{0}^{a} d^2*\sqrt{1-(sin\theta)^2} * cos\theta d\theta $
$ 1-sin^2\theta $는 항등식에 따라 $ cos^2\theta $와 같으니
$ T_1 = \int_{0}^{a} d^2*\sqrt{(cos\theta)^2} * cos\theta d\theta $
$ T_1 = \int_{0}^{a} d^2*cos\theta * cos\theta d\theta $
$ T_1 = \int_{0}^{a} d^2*cos^2\theta d\theta $
여기서 삼각함수의 제곱은 적분불가하므로 더 쉬운 형태로 바꿔주겠습니다.
cos 2배각을 이용하면
$ cos^2\theta = \frac{1+cos2\theta}{2} $ 이므로
$ T_1 = \int_{0}^{a} d^2*\frac{1+cos2\theta}{2} d\theta $
$ T_1 = \frac{d^2}{2}\int_{0}^{a} (1+cos2\theta) d\theta $
자, 여기서 변수치환 했으니 당연히 아래끝 위끝도 변경해줘야합니다.
여기서 y가 0일땐, $ \theta $도 0이므로 아래끝은 동일하게 0이고,
위끝이 a인 경우엔,
$ a = d*sin\theta $
$ \frac{a}{d} = sin\theta $
$ arcsin \frac{a}{d} = \theta $
로 정리되므로, 위끝 아래끝 바꿔서 최종식을 써보면
$ T_1 = \frac{d^2}{2}\int_{0}^{arcsin \frac{a}{d}} (1+cos2\theta) d\theta $가 되겠네요
$ T_1 = \frac{d^2}{2}(\int_{0}^{arcsin \frac{a}{d}} 1 d\theta + \int_{0}^{arcsin \frac{a}{d}} cos2\theta) d\theta $
$ T_1 = \frac{d^2}{2} ([\theta]^{arcsin \frac{a}{d}}_{0}+ \int_{0}^{arcsin \frac{a}{d}} cos2\theta) d\theta $
$ T_1 = \frac{d^2}{2} (arcsin \frac{a}{d} + \int_{0}^{arcsin \frac{a}{d}} cos2\theta) d\theta $
$ T_1 = \frac{d^2}{2} (arcsin \frac{a}{d} + [\frac{1}{2}sin2\theta]^{arcsin \frac{a}{d}}_{0}) $
여기서 sin 2t는 2sin t cos t와 같으므로
$ T_1 = \frac{d^2}{2} (arcsin \frac{a}{d} + [sin\theta cos\theta]^{arcsin \frac{a}{d}}_{0}) $
$ T_1 = \frac{d^2}{2} (arcsin \frac{a}{d} + sin(arcsin \frac{a}{d}) * cos(arcsin \frac{a}{d})) $
여기서 arcsin은 sin의 역함수이므로 $ f(f^{-1}(x)) = x $를 이용하여 $ sin(arcsin \frac{a}{d}) = \frac{a}{d} $
cos(arcsin)의 경우
$ \theta = arcsin \frac{a}{d} $
$ sin \theta = \frac{a}{d} $
$ sin^2\theta + cos^2\theta = 1 $
$ cos\theta = \sqrt{1-sin^2\theta} $
$ cos\theta = \sqrt{1-\left(\frac{a}{d}\right)^2} $ 로 정리되므로
$ T_1 = \frac{d^2}{2} (arcsin \frac{a}{d} + \frac{a}{d} \sqrt{1-\left(\frac{a}{d}\right)^2}) $
이 되며
결국 총 식은
$ T = \frac{d^2}{2} (arcsin \frac{a}{d} + \frac{a}{d} \sqrt{1-\left(\frac{a}{d}\right)^2}) - \frac{d}{2}a $
자, 이제 다 왔습니다.
$ \frac{1}{4}S = \frac{1}{2}A_{segment} + T $
$ \frac{1}{8}d^2(\pi - \sqrt{3}) = \frac{1}{4}d^2(\frac{\pi}{3} -\frac{\sqrt{3}}{2}) + \frac{d^2}{2} (arcsin \frac{a}{d} + \frac{a}{d} \sqrt{1-\left(\frac{a}{d}\right)^2}) - \frac{d}{2}a $
식이 복잡하니 정리해보죠.
일단 $ \frac{2}{d^2} $으로 양변 곱해줍니다.
$ \frac{1}{4}(\pi - \sqrt{3}) = \frac{1}{2}(\frac{\pi}{3} -\frac{\sqrt{3}}{2}) + (arcsin \frac{a}{d} + \frac{a}{d} \sqrt{1-\left(\frac{a}{d}\right)^2}) - \frac{a}{d} $
풀어서 상수항 정리하면,
$ \frac{\pi}{12} = arcsin(\frac{a}{d})+\frac{a}{d}\sqrt{1-\left(\frac{a}{d}\right)^2}-\frac{a}{d} $
이 식에서 a를 찾아주면 영점에서 얼만큼 위로 올라가서 가로선을 그어야 4등분이 되는지가 나오며, 이를 $ \frac{\sqrt{3}}{2}d-a $를 하면 삼각형의 위쪽 꼭지점(주황색)으로부터의 거리를 구할 수 있습니다.
참고로 이 방정식은 초월방정식이라 사람이 일반해를 구할수는 없고, 계산기의 도움을 빌려야합니다.이번에는 wolframalpha도 두손두발 들고 뻗어버렸기에, chatgpt를 이용하여 계산하면
gpt의 불확실한 결과(매번 결과가 달라지는)로 인해 다시 수식정리해서 wolframalpha로 계산하면
$ a = 0.268309283804244d $
로 결과가 나오고, $ \frac{\sqrt{3}}{2}d-a $이 식에 넣어 계산하면
0.597716119980195d
라는 결과가 나오게 됩니다.
3] 수식적 결론

결국 폭의 0.5977위치에서(삼각형의 꼭지점에서부터 0.5977d 위치에서) 가로로 한번, 이후 세로로 중앙을 한번 자르면 정확하게 이 뢸로삼각형을 4등분 할 수 있습니다.(전체 폭의 60%쯤 되는 위치네요. 위와같은 형태에선 정확한 절반보다 조금 아래라고 생각하시면 될 것 같습니다.)
마무리-
이 뢸로삼각형은 의외로 활용도가 꽤 있습니다. 벽을 네모나게 뚫는 드릴도 이 뢸로삼각형을 응용하고 있으며, 무엇보다 폭이 어디에서재도 같다는 성질은 아주 요긴하게 쓰일 수 있습니다.
가령 약을 만들때도, 이 뢸로 삼각형의 모양대로 타정하면 약이 어떤 슬라이드를 지나갈때 막힘없이 원과 비슷하게 흘러갈 수 있겠죠
그래서 실제로 시판되는 약중에서도 이 뢸로삼각형의 모양인 약들이 꽤 있습니다.
그중에 대표적인게 바라크루드(Baraclude)인데요, 실제로 약의 정보를 보면 가로 세로 높이가 같은 뢸로삼각형임을 알 수 있습니다.
0.5mg 제형의 경우 8.4mm의 폭을 가지는데, 이걸 계산한 결과에 대입하면
삼각형의 한 꼭지점에서부터 5mm떨어진 지점에서 가로로한번 세로로한번 자르면 된다는 결론이 나오죠.
'Study > Mathematics' 카테고리의 다른 글
| 사이클로이드의 면적구하기(면적분) (0) | 2024.11.17 |
|---|---|
| 직선 두개로 뢸로 삼각형(Reuleaux triangle) 4등분 하기[그러나 이제 적분이 없는] (0) | 2024.11.14 |
| [수학/패러독스] 아리스토텔레스의 바퀴 역설(Aristotle's wheel paradox) (0) | 2024.10.07 |
| 사이클로이드(Cycloid)의 길이 구하기(선적분) (0) | 2024.07.01 |
| 멱급수 전개(Power series expansion)로 피보나치 수열 풀기 (0) | 2024.06.30 |