사이클로이드 길이 구하기(선적분)
1. 사이클로이드?
사이클로이드라는 곡선을 아는가?

원에서 한 점을 찍고, 원이 한바퀴 구르는 동안 그 점의 궤적을 따라서 그리면 아주 독특한 곡선이 하나 만들어지는데 이를 사이클로이드라고 한다.
https://www.desmos.com/calculator/v3ouxovbkf?lang=ko
Cycloid
www.desmos.com
위 사이트에 접속하여 왼쪽 위의 a 부분을 잡고 슬라이드 해보면 원이 굴러가면서 만드는 자취란 것을 알 수 있다.
참고로 위 그래프에서 cycloid는 파란선이다.
사이클로이드는 최속강하이론(다른말로 공이 가장 빨리 내려오는 곡선)에 활용 되기도 하는데, 이 특이하고 신기한 성질은 다음에 알아보도록하고..
2. 사이클로이드 곡선 길이 구하기!
이 독특한 곡선의 길이를 구할 수 없을까?
원은 $ 2 \pi r $이지 않은가?
한번 구해보자!
2-1. 선적분
길이를 구하는 적분을 '선적분'이라고도 하는데, 원리는 간단하다.
아주 미소한 양의 증분 x와 y을 피타고라스 정리 써서 직선 거리를 구해내고, 이를 쭉~ 끝까지 적분해내는것이다.
그럼 결국 미소하게 변하는 x와 y를 따라서 어떤 아주아주아주 미세한 직선이 만들어질테고, 이 아주 미소한 직선을 다시 모았으니 곡선의 길이가 되겠다.
그러면 이 아주 미소한 x와 y는 어떻게 구하냐면.. 특정 식을 x에 대해서 미분하고 y에 대해서 미분하면 아주 미소한 x의 증분과 y의 증분이 나올 것이고, 이를 피타고라스 정리로 모으면 아주 미소한 직선이 하나 구해질 것이다. 식으로 쓰면
$ \sqrt{(dx)^2+(dy)^2} $
그리고 이것을 모으면 되는데,
$ \int \sqrt{(dx)^2+(dy)^2} $
아뿔싸! 적분은 '아주 미소한 어떤 것'을 '모은다'로 정의 되기 때문에, $ \int $과 'd어쩌구'가 세트로 나와야한다.
따라서, 우리는 가장 간단하게 'x에 대해서 모을거야' 라고 정의를 해주기 위해 dx를 원 식에서 뽑아내면
$ \int \sqrt{\left(\frac{dx}{dx}\right)^2+\left(\frac{dy}{dx}\right)^2} dx $
$ \int \sqrt{1+\left(\frac{dy}{dx}\right)^2} dx $
짜잔, 적분식 완성이다.
심지어 이 식이 매개변수로 나타나는 식이라면, 매개변수를 통한 미분으로도 정의할 수 있다.
여기서는 '미소한 x와 미소한 y를 미소한 매개변수로 나타냈을 때, 얘를 모을께!'니까
$ \int \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2} dt $
로 정의할 수 있겠다.
2-2. 매개변수 표현법
자, 이제 선의 길이를 구할 수있는 '도구'는 찾아내고 정의를 마쳤는데... 정작 이 사이클로이드의 한 점을 어떻게 x와 y로 표현할 수 있을 것인가!?
가장 쉬운 방법은 원이 어떤 각도 t만큼 돌아갔을 때 그 각도에 대해서 x와 y가 정의가 되므로 이를 이용하여 매개변수로 나타낼 수 있겠다!
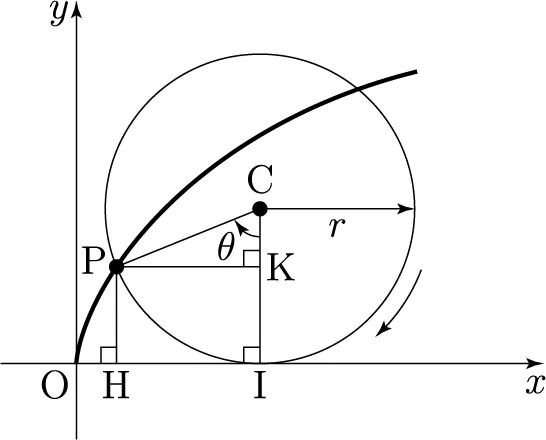
자, 가장 쉬운 y부터 보자, y는 원이 t만큼 돌아갔을 때(위 그림에서 $ \theta $), 반지름 r에 대해서 $ r - r cos t $만큼 움직인 것을 알 수 있겠는가?(위 그림에서 원이 $ \theta $만큼 돌아갔을 때 $ \overline{CI} - \overline{CK} $가 y의 위치임을 알 수 있다. 이를 $ \overline{CI} = r,\ \overline{CK} = r cos \theta $로 치환하면 바로 식이 나온다)
그럼 x는? 원이 t만큼 돌아갔을 때 원의 중심이 x축으로 이동한 거리는, 그 호의 길이와 같다. 왜냐고? 바닥에 원 둘레를 딱 붙이고 돌아갔을테니까!(위 그림에서 $ \overline{OI} = \overset{\mmlToken{mo}{⏜}}{\rm PI} $)
그러면 원의 중심은 $ r t $(위 그림에서 $ \overset{\mmlToken{mo}{⏜}}{\rm PI} = \overline{OI} $)만큼 움직였을 테고, 여기서 x는 $ r sin t $(위 그림에서 $ \overline{PK} $)만큼 원의 중심보다 뒤에 있을 테니 $ r t - r sin t $가 되겠다.
다시 쓰면
$ x = r t - r sin t = r(t-sin t) $
$ y = r - r cos t = r(1-cos t) $
자, 이렇게 x와 y좌표를 나타낼 수 있는 관계식도 찾았다! 그렇다면 이제 바로 선적분 들어가보자
2-3. 매개변수로 표현된 선적분 풀기!
$ dx = r(1-cos t) dt \Leftrightarrow \frac{dx}{dt} = r(1-cos t) $
$ dy = r sin t dt \Leftrightarrow \frac{dy}{dt} = r sin t $
$ \int \sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2} dt $
$ \int \sqrt{(r(1-cos t))^2+(r sin t)^2} dt $
근데 t가 0에서부터 $ 2 \pi $ 즉, 한바퀴 굴러갈때 거리를 잴거니까 적분의 위끝, 아래끝은 각각 0과 $ 2\pi $다.
$ \int_{0}^{2\pi} \sqrt{r^2((1-cos t)^2+(sin t)^2)} dt $
$ \int_{0}^{2\pi} r \sqrt{((1-cos t)^2+(sin t)^2)} dt $
$ r \int_{0}^{2\pi} \sqrt{((1-cos t)^2+(sin t)^2)} dt $
$ r \int_{0}^{2\pi} \sqrt{1-2cos t+(cos t)^2+(sin t)^2} dt $
$ r \int_{0}^{2\pi} \sqrt{1-2cos t+1} dt \leftarrow cos^2 x + sin^2 x = 1 $
$ r \int_{0}^{2\pi} \sqrt{2-2cos t} dt $
$ r \int_{0}^{2\pi} \sqrt{2(1-cos t)} dt $
$ r \int_{0}^{2\pi} \sqrt{2(1-(1-2(sin \frac{t}{2})^2)} dt \leftarrow cos(\frac{t}{2}+\frac{t}{2}) = cos^2 \frac{t}{2} - sin^2 \frac{t}{2} = 1 - 2sin^2 \frac{t}{2} $
$ r \int_{0}^{2\pi} \sqrt{2(2(sin \frac{t}{2})^2)} dt $
$ r \int_{0}^{2\pi} \sqrt{4(sin \frac{t}{2})^2} dt $
$ r \int_{0}^{2\pi} 2\sqrt{(sin \frac{t}{2})^2} dt $
$ 2r \int_{0}^{2\pi} \sqrt{(sin \frac{t}{2})^2} dt $
$ 2r \int_{0}^{2\pi} sin \frac{t}{2} dt $
$ 2r \left(-2 cos \frac{t}{2}\right]_{0}^{2\pi} $
$ 2r (-2 (-1 - 1)) $
$ 8r $
3. 결론
즉, 사이클로이드의 길이는 반지름의 8배, 지름의 4배 되겠다!
'Study > Mathematics' 카테고리의 다른 글
| 직선 두개로 뢸로 삼각형(Reuleaux triangle) 4등분 하기 (0) | 2024.11.12 |
|---|---|
| [수학/패러독스] 아리스토텔레스의 바퀴 역설(Aristotle's wheel paradox) (0) | 2024.10.07 |
| 멱급수 전개(Power series expansion)로 피보나치 수열 풀기 (0) | 2024.06.30 |
| 점화식에서의 특성방정식(characteristic equation) (87) | 2024.01.25 |
| 직선 두개로 원을 삼등분하기 (3) | 2022.03.19 |