사이클로이드(Cycloid)의 부피 구하기(회전체적분, 부피적분)
사이클로이드(Cycloid) 시리즈 목차
- 사이클로이드(Cycloid)의 길이 구하기 (선적분)
- 사이클로이드의 면적 구하기 (면적분)
- 사이클로이드(Cycloid)의 부피 구하기 (회전체적분, 부피적분)
- 사이클로이드(Cycloid) 회전체의 표면적(겉넓이) 구하기 (회전체적분, 겉넓이적분)
0. 서론
우리는 앞서 사이클로이드의 호의 길이(사이클로이드(Cycloid)의 길이 구하기(선적분))와 면적(사이클로이드의 면적구하기(면적분))을 구해보았습니다.
이번엔 세번째 시간으로 사이클로이드의 부피에 대해서 알아봅시다!
1. 부피?
사이클로이드는 2차원 평면에 있는데 왠 부피?라고 하신다면, 적분에는 항상 따라붙는 세가지가 선적분! 면적분! 회천체적분! 입니다.
즉, 2차원 평면에 있는 '면'을 x축 주위로 회전시키면 3차원 입체가 만들어지고, 그 부피를 적분으로 구할 수 있는거죠!
그리고 지금 우리는 이 사이클로이드를 x축을 기준으로 한바퀴 돌려서 소위 '럭비공'과 같은 모양으로 만들 예정입니다.
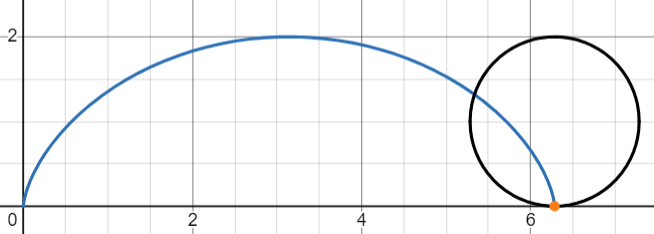
요렇게 생긴 곡선을

x축 기준으로 요렇게 회전시키는거죠.
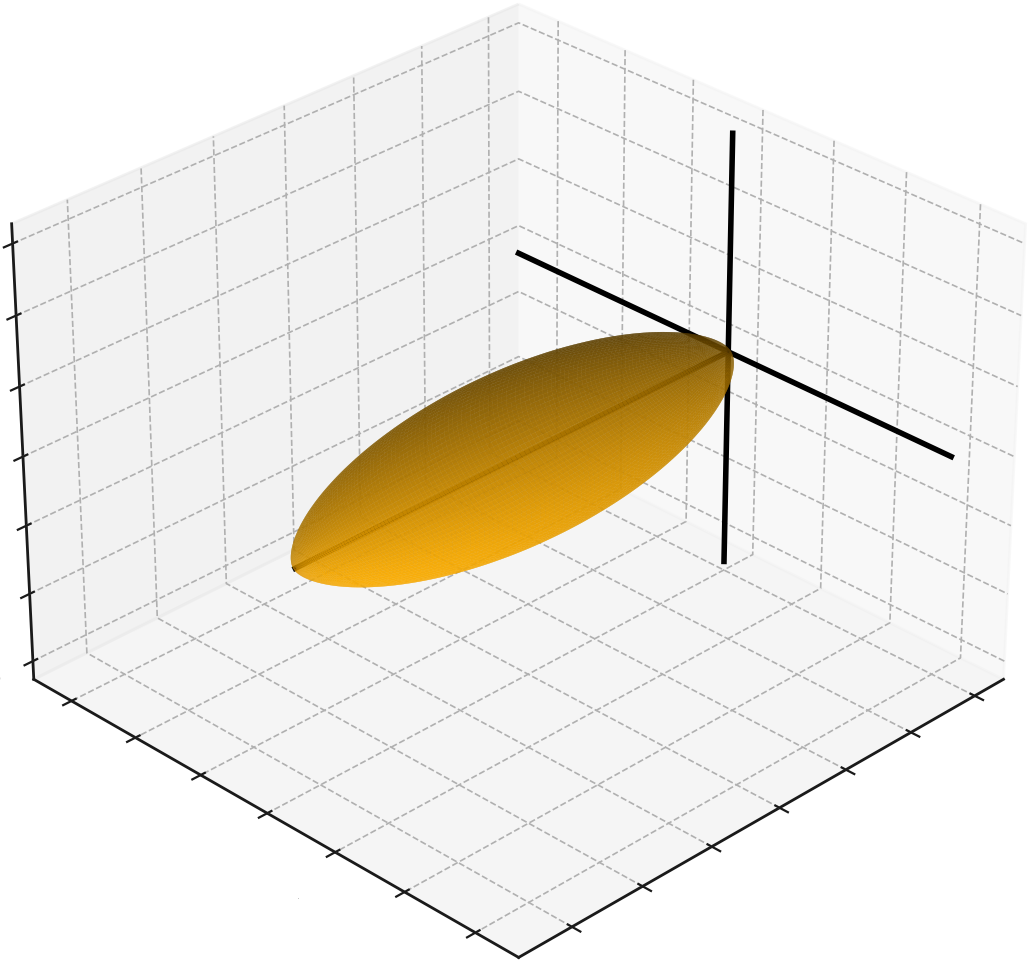
대략 3D로 보면 이런 느낌이겠죠?
2. 회전체의 부피 공식 설정
자, 일단 '회전'하면 그 단면은 항상 '원'이 되겠죠?
그럼 적분의 모토와도 같이, 면을 쫘좌좌좍 모아가면 부피가 되겠네요!(뭐, 엄밀히는 면*미소높이 하여 아주 작은 원통들을 모아가는 거겠지만요..)
일단 원의 넓이는 $ \pi r^2 $으로 정의됩니다. 여기서 $ r $은 반지름이죠.
우리는 현재, x축을 기준으로 한바퀴 돌려서 만들었으니, 반지름은 바로 이 곡선의 높이가 될 겁니다.
이전 포스팅에서 확인하실 수 있듯이 현재 이 곡선의 높이 y는 $ y = r(1-\cos t)$ 이렇게 정의 되어 있으므로,
회전체의 단면의 원의 넓이는 $ \pi r^2 = \pi (r(1-\cos t))^2$이 되겠네요.
그리고 여기서 아주 작은 미소부피(dV)를 구하기위해 원 넓이에다가 아주 미소한 높이를 곱해줘야 하겠습니다.
현재 회전체의 부피를 x축을 따라가며 구하고 있으므로 이 원통(원기둥)의 높이는 바로 $ dx $가 되겠네요.
즉, $ dV = \pi (r(1-\cos t))^2 dx $ 되겠습니다.
그리고 이 미소부피들을 싹 다 적분하면, 회전체의 부피가 나오겠죠?
즉, $ \int dV = \int \pi (r(1-\cos t))^2 dx $입니다.
그러나 여기서 본식은 매개변수 표현인데 바로 $ dx $를 써서 계산이 불가능 하기때문에, 과거 포스팅에서 정리했던 내용들을 다시 상기해보면, $ dx = r(1-\cos t)dt $입니다.
적분을 위한 준비는 끝났습니다. 다시한번 정리해보죠.
적분의 아래끝은 0 위끝은 $ 2 \pi $, $ y = r(1-\cos t)$, $ dx = r(1-\cos t)dt $
이제 이걸 이용해서 수식으로 정리해주면,
$ V = \int_0^{2 \pi} dV = \pi \int_0^{2 \pi} (r(1-\cos t))^2 r(1-\cos t) dt $
이렇게 정리가 되겠습니다.
수식은 다 세워졌네요. 이제 정리하며 풀기만하면 끝입니다.
3. 적분 계산
$ \pi \int_0^{2 \pi} (r(1-\cos t))^2 r(1-\cos t) dt $
이 수식을 다시 깔끔하게 정리하면
$ \pi r^3 \int_0^{2 \pi} (1-\cos t)^3 dt $
요렇게 세제곱 형식으로 묶을 수 있을겁니다.
그리고 세제곱을 다시 풀어주면
$ \pi r^3 \int_0^{2 \pi} (1-3\cos t+3\cos^2 t-\cos^3 t) dt $
이렇게 풀 수 있고,
삼각항수 항등식에서 $ \cos^2 t = \frac{1 + \cos 2t}{2} $ 이므로
$ \pi r^3 \int_0^{2 \pi} (1-3\cos t+\frac{3}{2}(\cos 2t+1)-\cos^3 t) dt $
$ \pi r^3 \int_0^{2 \pi} (\frac{5}{2}-3\cos t+\frac{3}{2}\cos 2t-\cos^3 t) dt $
이렇게 정리가 되겠군요.
이제 적분은 선형결합에 대해 분배될 수 있으므로,
$ \pi r^3 \left( \int_0^{2 \pi} \frac{5}{2} \ dt-3\int_0^{2 \pi} \cos t \ dt+\frac{3}{2}\int_0^{2 \pi}\cos 2t \ dt-\int_0^{2 \pi} \cos^3 t \ dt \right) $
여기서, $ \cos^3 t $는 직접적으로 적분할 수가 없으니, 찢어줍시다.
$ \pi r^3 \left( \frac{5}{2} \int_0^{2 \pi} dt-3\int_0^{2 \pi} \cos t \ dt+\frac{3}{2}\int_0^{2 \pi}\cos 2t \ dt-\int_0^{2 \pi} \cos^2 t \cdot \cos t \ dt \right) $
이러면 약간의 빛이 보입니다. 삼각항수 항등식 $ \cos^2 t + \sin^2 t = 1 \Leftrightarrow \cos^2 t = 1-\sin^2 t $을 쓰면
$ \pi r^3 \left( \frac{5}{2} \int_0^{2 \pi} dt-3\int_0^{2 \pi} \cos t \ dt+\frac{3}{2}\int_0^{2 \pi}\cos 2t \ dt-\int_0^{2 \pi} (1-\sin^2 t) \cdot \cos t \ dt \right) $
그리고 $ \sin t $를 $ u $로 치환하면, 사실 치환한 아래끝 위끝이 모두 값이 0이 되면서 적분결과가 0이 되어버리지만 조금 더 수학적 재미를 위해 끝을 임의로 놓고 계산진행해보겠습니다.(구조를 보기 위해 양 끝에 임의기호 @, * 사용)
$ \pi r^3 \left( \frac{5}{2} \int_0^{2 \pi} dt-3\int_0^{2 \pi} \cos t \ dt+\frac{3}{2}\int_0^{2 \pi}\cos 2t \ dt-\int_{@}^{*} (1-u^2) du \right) \leftarrow u = \sin t,\ du = \cos t dt $
$ \pi r^3 \left( \frac{5}{2} \int_0^{2 \pi} dt-3\int_0^{2 \pi} \cos t \ dt+\frac{3}{2}\int_0^{2 \pi}\cos 2t \ dt-(\int_{@}^{*} du - \int_{@}^{*} u^2 du) \right) $
$ \pi r^3 \left( \frac{5}{2} \int_0^{2 \pi} dt-3\int_0^{2 \pi} \cos t \ dt+\frac{3}{2}\int_0^{2 \pi}\cos 2t \ dt-(u\vert_{@}^{*} - \frac{1}{3} u^3\vert_{@}^{*}) \right) $
$ \pi r^3 \left( \frac{5}{2} \int_0^{2 \pi} dt-3\int_0^{2 \pi} \cos t \ dt+\frac{3}{2}\int_0^{2 \pi}\cos 2t \ dt- \left( \sin t \vert_0^{2\pi} - \frac{1}{3} \sin^3 t \vert_0^{2\pi} \right) \right) \leftarrow u = \sin t $ (+치환에서 다시 돌아왔으니 적분구간 다시 전과 같은 구간으로 살려주기)
여기서 바로 $ \sin t $에 값 대입하면 0 나오지만, 그냥 수식 그대로 끌고가 볼께요. 이제 다 적분해줍니다.
$ \pi r^3 \left( \frac{5}{2} t \vert_0^{2 \pi} -3 \sin t \vert_0^{2 \pi}+\frac{3}{4}\sin 2t\vert_0^{2 \pi} \ dt- \sin t \vert_0^{2\pi} + \frac{1}{3} \sin^3 t \vert_0^{2\pi} \right) $
적분 풀면
$ \pi r^3 \left( \frac{5}{2} \cdot 2\pi-0+0-0+0 \right) $
즉, 살아 남은 항은 첫번째 항 뿐이므로
$ 5 \pi^2 r^3 $
이 됩니다.
사실 모든게 0으로 정리되는 걸 보여드리고 싶어 이렇게 진행했는데, 사실... 0에서 $ 2\pi $까지 $ \cos $함수의 홀수승 적분은 전부 0이라서
$ \pi r^3 \left( \int_0^{2 \pi} \frac{5}{2} \ dt-3\int_0^{2 \pi} \cos t \ dt+\frac{3}{2}\int_0^{2 \pi}\cos 2t \ dt-\int_0^{2 \pi} \cos^3 t \ dt \right) $
이렇게 정리된 순간 $ \cos $적분은 전부 사라지니 사실상 이 단계에서 계산이 끝난거나 다름없긴 합니다...
4. 결론
사이클로이드 회전체의 부피 $ V $ 는 $ 5 \pi^2 r^3 $입니다.
'Study > Mathematics' 카테고리의 다른 글
| [수학/패러독스] 동전을 굴리면 더 많이 굴러간다? – 동전 역설(Coin Paradox) (0) | 2025.07.15 |
|---|---|
| 사이클로이드(Cycloid) 회전체의 표면적(겉넓이) 구하기(회전체적분, 겉넓이적분) (0) | 2025.07.13 |
| 연산의 정의부터 군, 환, 체까지 – 닫힘성에서 시작하는 대수 구조의 세계 (0) | 2025.07.08 |
| 모츠킨 수열(Motzkin sequence) (0) | 2025.07.07 |
| 신입생의 꿈과 대학교 2학년의 꿈(Freshman's dream & Sophomore's dream) (0) | 2025.07.06 |