무한서고

[수학/패러독스] 아리스토텔레스의 바퀴 역설(Aristotle's wheel paradox)

말머리-

안녕하세요 여러분!

오랜만에 글감을 들고 찾아왔습니다.

오늘 소개드릴 내용은 바로 '바퀴 역설' 혹은 'Wheel paradox'라는 건데요

도대체 뭐가 '역설'일까요?

소개시켜드리겠습니다!

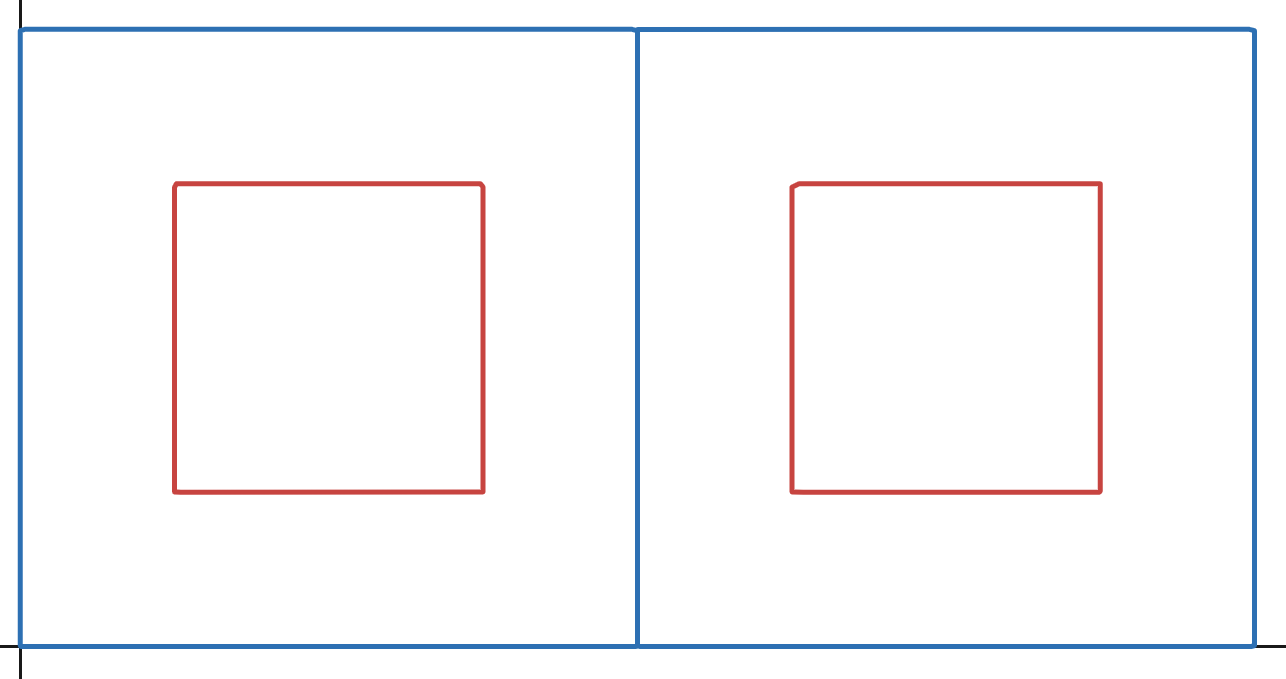
위 이미지가 보이시나요?

이미지에는 큰 바퀴(파란색)과 그 안에 고정된 작은 바퀴(빨간색)이 있습니다.

이 두 바퀴는 따로 떼서 굴려보면 딱 그 바퀴의 원주(원 둘레)만큼 굴러가며 딱 한바퀴를 돌 겁니다.

그! 런! 데!

이 두 바퀴를 정 가운데 딱 붙여서 굴리는 순! 간!

큰 바퀴가 한바퀴 굴러갈 때, 그 거리만큼 작은 바퀴도 딱 한바퀴 도는 일이 발생하는 것이죠!

두 바퀴가 동시에 굴러갈 때, 큰 바퀴가 굴러간 거리 만큼 작은 바퀴도 같은 거리를 이동하는 겁니다!

아니 어떻게 이런일이!?

분명 떼어 놓으면 한바퀴 도는 거리가 다른데, 붙이면 같아진다!?

그래서 이것이 바로 역설(paradox), 패러독스입니다.

참고로 기원전 학자인 아리스토텔레스(Aristotle)의 이름이 붙은 만큼 엄청 오래된 역설이라는 거죠!

[더불어 제논의 역설도 고대 그리스에서 나온 걸 보면 역시 철학의 시대가 아니었나 싶네요]

그럼 도대체 이런 문제가 발생하는 이유는 뭘까요? 원인부터 살펴봅시다.

원인-

자, 이 문제를 해결하려면 원인을 일단 잘 살펴봐야겠죠?

1) 사이클로이드로 생각해보기

자 일단 사이클로이드가 궁금하시다면 >>여기<<에서 관련 내용을 한번 살펴보시기 바랍니다.

간단하게 말해 원에서 점 하나 찍고 그 원의 궤적을 보는게 사이클로이드입니다.

그렇다면 큰원에 점을 찍고, 작은 원에 점을 찍고 그 궤적을 본다면?

요런 자취가 나올겁니다. 자취는 점선으로 나타나있어요.

잘 보면 파란 자취와 빨간 자취가 다르죠?

그러니까 뭔가 운동이 다를 거라는 걸 암시하죠

보면 파란색 점선이 위아래로 더 많이 움직이고, 빨간색 점선은 위아래로 덜 움직이는데, 결국 총 이동한 거리는 같다고 한다면 당연히 빨간색이 좀 더 '효율적'으로 움직인 거니 수평방향으로 더 많이 움직였다는 사실을 도출해 낼 수 있습니다.

그러나 뭔가 조금 찝찝하죠?

2) 다각형으로 생각해보기

원은 다른말로 '무한각형'이라고도 합니다.

실제로 삼각형>사각형>오각형>... 이런식으로 각형을 늘려나가다보면 점점 원에 가까워지는 모습을 볼 수 있는데요

그렇다면 원에서의 문제이니까 각형을 줄여봅시다!

무한에서 줄이고 줄여서~~~ 사각형으로 가보죠!

자, 이런 네모바퀴가 굴러가는걸로 생각해봅시다.

이 네모바퀴는 총 네번을 굴러 가면 한바퀴를 돌 겁니다.

근데, 자세히보면, 큰 네모는 딱 붙어서 도는데, 작은 네모는 공간이 떨어져있네요?

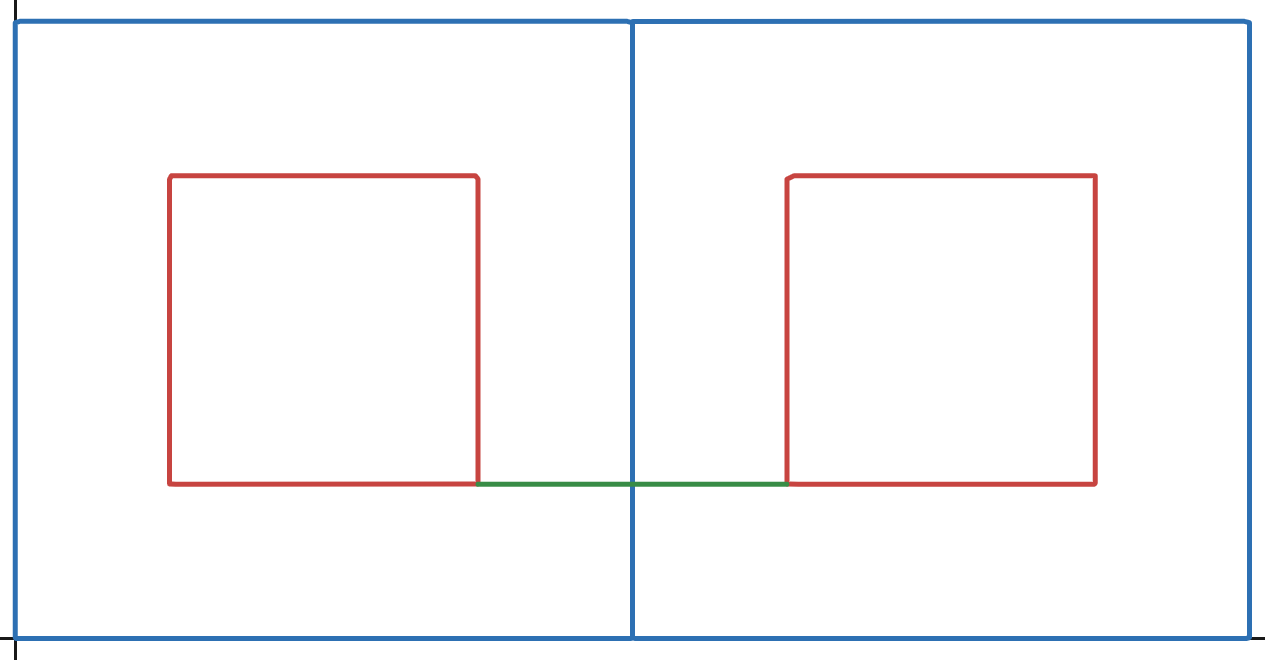
요 초록 선 만큼요

아... 이제 감이 올 것 같습니다.

이 안에 있는 바퀴는 공간을 점프해서 이동하는 거였군요!?

그래서 큰 바퀴가 딱 한바퀴 도는동안 같은 거리를 이동할 수 있었던 거네요!

여기서 오각형>육각형 등 각수를 계속 늘려가면 이 초록선은 점점 짧아지겠지만, 더욱 많아지겠고, 사라지지는 않겠군요!

그렇다면 원은!? 아주 미세하게 이 초록선들이 거의 점으로 분포되어 보이지 않는 걸겁니다!

아하! 해결했습니다! 너무 미세해서 보이지 않지만 있다!

그럼 원은 '점프'라기보다는 아주아주 미세하게 '미끄러진다'라고도 볼 수 있겠네요?

(그러나 실제는 너무너무 작아서 얘가 점프를 하는지 미끄러지는지는 알기 어렵겠죠?)

자, 그럼 왠지 이 길이를 구하고 싶어지지 않나요?

수식으로 한번 풀어보죠!

이 애매한 거리를 수식으로 풀어보기!-

자자, 이제 수식으로 풀어보려고 하니까 일단 한가지 생각해보죠

어떤 n각형이 한 변에서 다른 변으로 돌때 돌아가는 각도는 그 n각형의 외각과 같습니다.

가령 삼각형은 120도를 돌아가 다음 변으로 돌아가겠고, 위에서 봤듯이 사각형은 90도를 돌면 다음 변으로 돌아갑니다.

마찬가지로 오각형은 72도를 돌면 다음 변으로 돌아가겠네요!

어.. 각형이 작아질수록 다음 변까지 돌아가는 각도가 작군요!

이를 수식으로 써보면 $ \theta = \frac{360}{n} $일겁니다.

좀 더 보기 편하게 60분법 각도를 호도법(radian)으로 바꿔주면, $ \theta = \frac{2 \pi}{n} $이 되겠네요.

자 그럼 도형에 열심히 보조선을 그어봅시다!

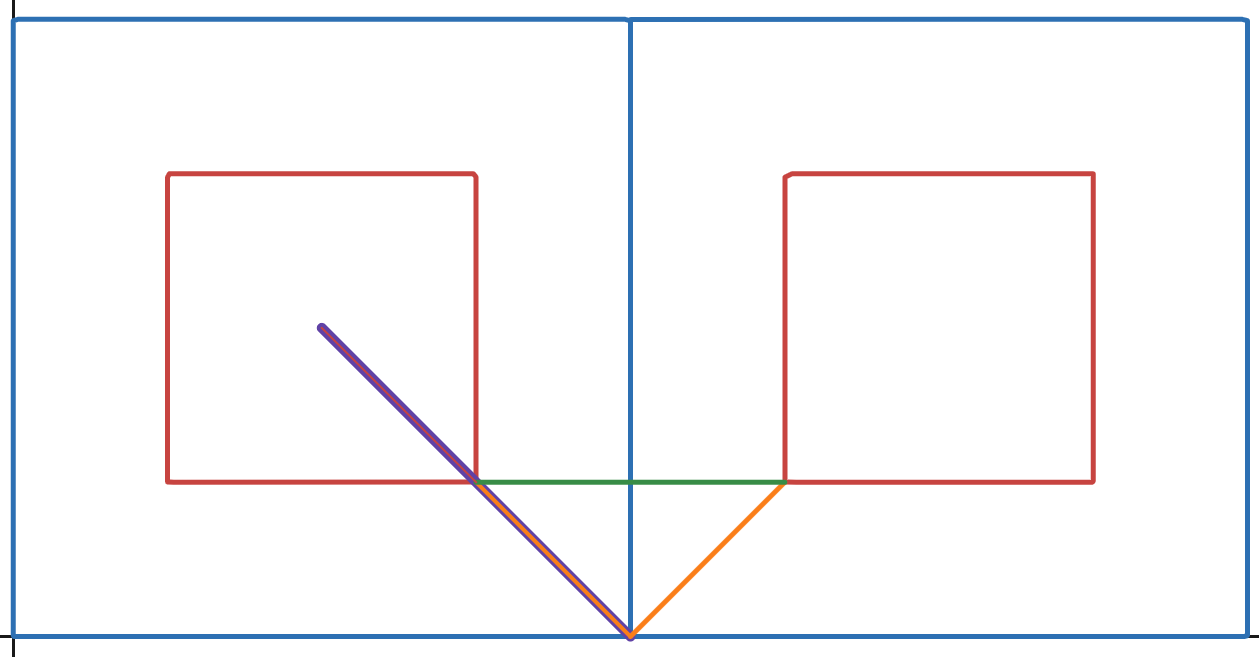
자, 여기 보라색선은 큰 바퀴의 반지름(이 될 예정인)입니다. (이를 a라고 하죠)

빨간색 바퀴의 안에 그려진 빨간색 선 또한 작은 바퀴의 반지름일 것입니다. (이를 b라고 해보겠습니다)

그리고 주황색 선은 큰 바퀴의 반지름-작은 바퀴의 반지름이죠 ( a-b 겠네요)

왜 저 주황색 선을 만들었냐면~ 초록색 선의 길이를 알고 싶기 때문이죠!

그리고 n각형의 바퀴는 한 변만큼 돌아갈 때 $ \theta $만큼의 각도로 돌아간다고 이미 정의를 했고, 주황색 선도 마찬가지로 $ \theta $만큼 돌겠죠

자, 각도와 변이 나오면 뭘 할 수 있다? 바로 삼각함수로 다른 변을 구할 수 있다!

일단 $ \theta $와 주황색 선 만으로는 바로 초록색 선의 길이를 구할 수 없으니 뭐든지 반을 똥강내봅시다.

일단 초록색 선의 반을 구하고 싶다면, 주황색 선 * $ \theta $의 절반을 하면 될 겁니다 수식으로 써보죠

근데 자꾸 무슨색 선~하니까 좀 헛갈리네요! 다시정의하죠

초록샌 선은 결국 우리가 구하고 싶은 선이니까 x라고 합시다

주황색 선은 a-b

돌아가는 각도 = 주황색 선의 각도 = $ \theta $

자, 전체 x길의 반은 (a-b)에다가 $ \theta $ 절반의 sin값을 곱해주면 나오게 되겠네요

$ \frac{x}{2} = (a-b)sin (\frac{\theta}{2}) $

자, 근데 저희는 $ \theta $를 아까 $ \frac{2 \pi}{n} $이라고 했으니

$ \frac{x}{2} = (a-b) * sin (\frac{2\pi}{2n}) $

$ \frac{x}{2} = (a-b) * sin (\frac{\pi}{n}) $

자, 왼쪽에 자꾸 2로 나누어져 있으니까 이제 양변에 2를 곱해서 전체 x길이에 대한 수식으로 바꿔보죠

$ x = 2(a-b) * sin (\frac{\pi}{n}) $

아, 근데 우리는 초록선 '단 하나'만 구했네요? 초록선은 바퀴가 n번 돌아 한바퀴 돌때까지 n개가 생기니까...

수식 복잡하게 하지말고 다시 정리하죠 $ n*x = L $이라고 새로 정의해봅시다. 초록선 n개가 모인걸 대문자 L로 놓을께요

$ L = 2*(a-b)*sin(\frac{\pi}{n})*n $

자 이제 어떤 n각형에 대해서 작은 바퀴가 점프하는 거리를 구하는 식이 완성되었습니다.

근데 아까 원은 무슨각형이다? 무한각형!

그럼 n이? 무한대!

근데 여기서 그냥 무한대 사용하면 수식이 '아니 뭐가 뭐지?'싶어지니 정리를 조금 해봅시다!

정말 재밌는 수식이 있는데요

$ \lim\limits_{x \to \infty} \frac{sin x}{x} $

는 뭐게요?

답은 1이랍니다! 그러므로!

$ L = 2*(a-b)*sin(\frac{\pi}{n})*n \Leftrightarrow L = 2*(a-b)*sin(\frac{\pi}{n})*n*\frac{\pi}{n}*\frac{1}{\frac{\pi}{n}} $

$ L = 2*(a-b)*\frac{sin(\frac{\pi}{n})}{\frac{\pi}{n}}*n*\frac{\pi}{n} $

$ L = 2*(a-b)*\frac{sin(\frac{\pi}{n})}{\frac{\pi}{n}}*\pi $

자, 항등식을 이용한 식변형을 했구요

이제 $ \lim\limits{x \to \infty} \frac{sin x}{x} $ 요 꼴이 나왔으니 바로 극한을 걸어봅시다.

$ L = \lim\limits{x \to \infty} 2*(a-b)*\frac{sin(\frac{\pi}{n})}{\frac{\pi}{n}}*\pi $

$ L = 2*(a-b)*\pi $

$ L = 2\pi(a-b) $

원에서 가칭 '점프하는 구간'의 길이를 구했습니다!

그리고 정말 신기하게도 큰 원의 원주길이($ 2\pi a $)에서 작은 원의 원주길이($ 2\pi b $)를 뺀만큼이 점프하는 구간이라는 답이 나왔네요!

결론-

결국, 안쪽의 원은 아주 조금씩 모종의 방법으로 이동하며 큰 원이 움직이는 만큼을 따라가고 있었던 것이었습니다 여러분!!

피보나치 수열의 일반항과 비율의 극한(황금비)

피보나치 수열하면 모르는 사람이 없을 정도로 아주 간단한 규칙을 가진 수열이다.

바로 앞의 두 숫자를 더하면 다음 숫자가 나오는 수열이다.

여기서 앞의 두 숫자는 1, 1 이다.

그러면 바로 아래와 같은 수열이 나오게 된다.

1 1 2 3 5 8 13 ...

물론 이 수열의 극한은 무한대로 발산할 것이 분명하지만, 이 수열의 두 항의 '비율'의 극한은 수렴할까? 수렴한다면 어디로 수렴할까? 한번 확인해보자.

여기서 수열의 극한을 확인하려면 항상 일반항이 있어야 한다. 그러나 피보나치 수열은 '앞의 두 수를 더하면 다음 숫자가 된다'는 점화식만 있는 형태이다. 그러면 이 점화식을 통해서 일단 피보나치 수열의 일반항을 구해보도록 하자.

피보나치 수열의 일반항 구하기

1. 피보나치 수열의 점화식을 써보자.

  피보나치 수열은 이 전의 두 항을 더하면 다음 항이 되는 수열이다.

  $ a_{n+2} = a_{n+1} + a_{n} $

  이러한 형태 점화식만 있는 상태로 등차, 등비, 멱급수 등등등 그 어떤 수열의 형태도 아니다.

2. 일반식으로 확장

  이 수열의 상태만으로는 우리가 뭔가 찝쩍거릴 건덕지가 없으니까, 일반적인 일반식으로 확장한 뒤 근과 계수와의 관계(Vieta's formulas, 두 근을 $ \alpha, \; \beta $로 놓으면 $ px^2+qx+r=0 $의 방정식에서 $ \alpha + \beta = - \frac{q}{p}, \alpha \beta = \frac{r}{p} $의 관계가 생긴다는 공식)를 활용하여 근을 활용한 일반식으로 변화시켜 볼 것이다. 참고로 수열에서 항수는 차수가 다른 방정식과 동일하게 볼 수 있다.(더 자세한 내용은 >>점화식에서의 특성방정식(characteristic equation)<<에서 확인할 수 있다.)

  $ a_{n+2} = a_{n+1} + a_{n} \Rightarrow x^2 = x + 1 \Leftrightarrow x^2 -x -1 = 0 $와 같이 쓴뒤, $ px^2+qx+r=0 $의 일반식으로 변환시켜주면, $ p = 1, q = -1, r = -1 $이 되고, 근과 계수와의 관계에서 $ \alpha+\beta=-\frac{q}{p}=1, \; \alpha \beta = \frac{r}{p} = -1 $이다.

  이는 다시 쓰면, $ p $가 기본적으로 1이기 때문에 $ \alpha+\beta = -q, \; \alpha \beta = r $이라고 놓을 수 있다.

  그래서 일반식을 다시 근과 계수와의 관계를 이용하여 계수가 아닌 근의 형태로 표현해주면

  $ x^2-(\alpha+\beta)x+\alpha \beta = 0 $

  이를 다시 수열의 항을 통해서 표현해주면

  $ a_{n+2} = (\alpha+\beta)a_{n+1} - \alpha \beta a_n $과 같은 근을 활용한 일반식으로 확장이 되었다.

  이때, $ a_1 = 1, \; a_2 = 1, \; \alpha + \beta = 1, \; \alpha \beta = -1 $이다.

3. 반복되는 형태를 만들어서 계산가능하게 만들자

  과거 >>https://omnil.tistory.com/172<<포스팅에서 감마함수를 팩토리얼로 변환하는 과정과 같이 등식의 좌변과 우변이 반복되는 형태를 만들어주게 되면 계산이 되지 않을 것 같은 등식도 계산이 된다. 특히 최종단계를 우리가 직접 계산해서 값을 알 수 있다면 더더욱이 말이다. 참고로 감마함수는 n=1일때 값이 1이며, 우리는 뭔가 이런단계를 거치면 1항이 1, 2항이 1이라는 것을 통해서 값을 구할 수 있을 것이다.

  $ a_{n+2} = (\alpha+\beta)a_{n+1} - \alpha \beta a_n $

  $ a_{n+2} = \alpha a_{n+1} + \beta a_{n+1} - \alpha \beta a_n $

  $ a_{n+2}-\alpha a_{n+1} = \beta a_{n+1} - \alpha \beta a_n $

  $ a_{n+2}-\alpha a_{n+1} = \beta (a_{n+1} - \alpha a_n) $

  이렇게 변환하면 등식의 좌변과 우변의 공동되는 부분의 한 항 차이가 $ \beta $배라는 것을 알 수 있다. 바로 이것으로 우리가 아는 $ a_2 $와 $ a_1 $를 가지고 계산할 수 있는 형태로 반복계산이 가능하다.

  $ a_{n+2}-\alpha a_{n+1} = \beta (a_{n+1} - \alpha a_n) $

  $ a_{n+1}-\alpha a_{n} = \beta (a_{n} - \alpha a_{n-1}) $

  $ \Rightarrow a_{n+2}-\alpha a_{n+1} = \beta^2 (a_{n} - \alpha a_{n-1}) $

  이런식으로 $ \beta $배씩 곱해주면 우항을 a2와 a1항으로 계산할 수 있는 형태로 만들어줄 수 있다.

  이 때, $ \beta $가 몇개 생기는지는 항 수를 보고 생각하면 된다.

  우변의 맨 오른쪽항이 a2항에서 a1항으로 떨어지게 되면, $ \beta $는 한개가 생길 것이다. 즉, an항에서 a1항으로 떨어지면 (n-1)개의 $ \beta $가 생성될 것이다.

  $ a_{n+2}-\alpha a_{n+1} = \beta \cdot \beta^{n-1} \cdot (a_{2} - \alpha a_1) $

  $ a_{n+2}-\alpha a_{n+1} = \beta \cdot \beta^{n-1} \cdot (1 - \alpha \cdot 1) \leftarrow \because a_2=1,\; a_1=1 $

  $ a_{n+2}-\alpha a_{n+1} = \beta \cdot \beta^{n-1} \cdot \beta \leftarrow \because \alpha + \beta = 1 $

  $ a_{n+2}-\alpha a_{n+1} = \beta^{n+1} $

  즉  $ a_{n+2}-\alpha a_{n+1} $는 $ \beta $를 $ n+1 $번 곱한 것이니 항수 만큼 $ \beta $를 곱해주는 횟수가 된다는 것을 알 수 있다. 그렇다면 우리가 알고싶은 $ a_n $을 기준으로 하는 식으로 바꿔주면

  $ a_{n}-\alpha a_{n-1} = \beta^{n-1} \cdots (1)$

  이 되고, 이는 $ \alpha $ 변수와 $ \beta $ 변수를 바꾸어도 변수위치만 바뀐 동일한 식이 나온다.

  $ a_{n}-\beta a_{n-1} = \alpha^{n-1} \cdots (2)$

4. 연립하여 $ a_n $에 대한 일반항으로 풀어준다.

  변수 두개에 식이 두개가 나왔으니 연립방정식으로 풀 수 있다.

  (2)식에 $ \frac{\alpha}{\beta} $배를 해준 뒤 (1)-(2)식을 해줘서 $ a_{n-1} $항을 소거하여 $ a_n $의 일반항을 얻을 수 있다.

  $ a_{n}-\alpha a_{n-1} = \beta^{n-1} \cdots (1)$

  $ \frac{\alpha}{\beta}a_{n}-\alpha a_{n-1} = \frac{\alpha^{n}}{\beta} \cdots (2)$

  $ (1)-(2) $

  $ a_{n}-\frac{\alpha}{\beta}a_n = \beta^{n-1}-\frac{\alpha^n}{\beta} $

  $ \beta a_{n}-\alpha a_n = \beta^{n}-\alpha^n $

  $ (\beta -\alpha) a_n = \beta^{n}-\alpha^n $

  $ \therefore a_n = \frac{\beta^{n}-\alpha^n}{\beta -\alpha} $

  일반항 겟!!

  이제 일반항에 값만 대입해주면 진짜 n에 몇번째 항인지만 대입해주면 거기에 해당하는 값이 나오는 일반항이 된다.

5. $ \alpha $와 $ \beta $의 값 구하여 일반항에 대입하기

  여기서 $ \alpha $와 $ \beta $는 사실 $ x^2 -x -1 = 0 $의 두 근과 같기 때문에 근의 공식을 통하여 바로 값을 구할 수 있다.

  $ ax^2+bx+c = 0 $에서 두 근은 $ \frac{-b\pm \sqrt{b^2-4ac}}{2a} $식으로 구할 수 있다.
  $ \frac{1\pm \sqrt{5}}{2}, \; a=1, \: b=-1, \: c=-1 $

  $ \beta = \frac{1 + \sqrt{5}}{2}, \; \alpha = \frac{1 - \sqrt{5}}{2} $

  $ a_n = \frac{\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n}{\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2}} $

  $ \therefore a_n = \frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right) $

  이렇게 피보나치 수열의 일반항을 구했다!!

  근데, 유리수의 합으로 나타나는 피보나치 수열에서 일반항에 무리수가 들어가는 것이 신기하지 않은가!

피보나치 수열의 비율의 극한

이렇게 일반항을 구했으면 비율의 극한도 쉽게 구할 수 있다.

여기서는 더 큰수를 더 작은수로, 즉 $ \frac{a_{n+1}}{a_n} $의 비를 구할 것이다.

이번엔 비율을 구할 것이기 때문에, 숫자까지 들어간 일반항 보다는 문자로 표현된 더 한눈에 보기 간편한 일반항을 사용하여 극한을 구해볼 것이다.

1. 비율 식 구하기

  $ a_{n+1} = \frac{\beta^{n+1}-\alpha^{n+1}}{\beta -\alpha} $

  $ a_{n} = \frac{\beta^{n}-\alpha^{n}}{\beta -\alpha} $

  $ \frac{a_{n+1}}{a_n} = \frac{\frac{\beta^{n+1}-\alpha^{n+1}}{\beta -\alpha}}{\frac{\beta^{n}-\alpha^{n}}{\beta -\alpha}} $

  $ \frac{a_{n+1}}{a_n} = \frac{\beta^{n+1}-\alpha^{n+1}}{\beta^{n}-\alpha^{n}} $

  $ \frac{a_{n+1}}{a_n} = \frac{\beta-\alpha \left(\frac{\alpha}{\beta}\right)^n}{1-\left(\frac{\alpha}{\beta}\right)^{n}} $

2. 극한 씌워주기

  $ \lim_{n \to \infty} \frac{a_{n+1}}{a_n} = \lim_{n \to \infty} \frac{\beta-\alpha \left(\frac{\alpha}{\beta}\right)^n}{1-\left(\frac{\alpha}{\beta}\right)^{n}} $

  여기서 $ \beta = \frac{1 + \sqrt{5}}{2}, \; \alpha = \frac{1 - \sqrt{5}}{2} $이고, $ \beta $가 $ \alpha $보다 크기 때문에 $ \left(\frac{\alpha}{\beta}\right)^n $항은 $ n $이 무한대로 갈 때 값이 0으로 수렴한다.

  참고로 실제 값을 대입해서 계산해본 $ \left(\frac{\alpha}{\beta}\right) $ 값은 $ \frac{\sqrt{5}-3}{2} $이며, 그 값은 약 -0.382이다. 즉, 이 값을 무한대로 제곱할 경우 양과 음을 반복 진동하며 수렴한다.

  즉, 극한을 취한 뒤의 값은

  $ \lim_{n \to \infty} \frac{a_{n+1}}{a_n} = \frac{\beta-\alpha 0}{1-0} $

  $ \lim_{n \to \infty} \frac{a_{n+1}}{a_n} = \beta $

  $ \therefore \beta $

  이며, 이 $ \beta $값은  $ \frac{1 + \sqrt{5}}{2} $이므로, 피보나치 수열의 비율의 극한 값은 $ \frac{1 + \sqrt{5}}{2} $이 된다.

  그러면 이 값은 과연 무엇일까

황금비

  인생을 살면서 '황금비'라는 단어를 한번은 들어본다.

  황금비는 1: 1.618로써 근사하면 5:8정도의 비율을 나타내는 것을 황금비라고 한다.

  이것은 우리가 어떤 비율을 봤을 때 가장 아름답다고 생각하는 비율이라고 하는데, 이 1.618이라는 값은

  $ \frac{1 + \sqrt{5}}{2} $을 계산하면 나오는 값이다.

  즉, 피보나치 수열의 비율을 극한으로 가져가면 황금비를 가진다는 사실!