무한서고

직선 두개로 뢸로 삼각형(Reuleaux triangle) 4등분 하기[그러나 이제 적분이 없는]

[나야 기하학]

말머리-

어제 뢸로 삼각형을 해체했다는 기쁨도 잠시... 어제 포스팅 쓰면서 적분 변환하느라 아주 길고 긴 latex을 작성했던 것이 떠올랐다.

근데 적분 말고, 전에 원을 나눌때도 기하학으로 하면 더 편했던 것 처럼 기하학으로는 안될까..?

싶었는데... 고민해보니 되긴하네!? 해서 시작한 포스팅이네요

하다보니 항이 많고, 원 변수를 모두 포함해서 계산하자면 아주 복잡해지는데 이를 적당히 간단한 변수로 치환치환 해가며 정리하면 금새 수식이 정리되는게, 정말 복잡한 적분 없이 바로 결과식에 도달하는게 재미지네요!

수식세우기-

1] 도형 나누기

이전 포스팅인 >>적분으로 뢸로삼각형 4등분하기<<를 기본으로 보시면 좋습니다.

기본 뼈대는 같습니다. 뢸로삼각형 넓이의 $ \frac{1}{4} $을 구하는 거지요.

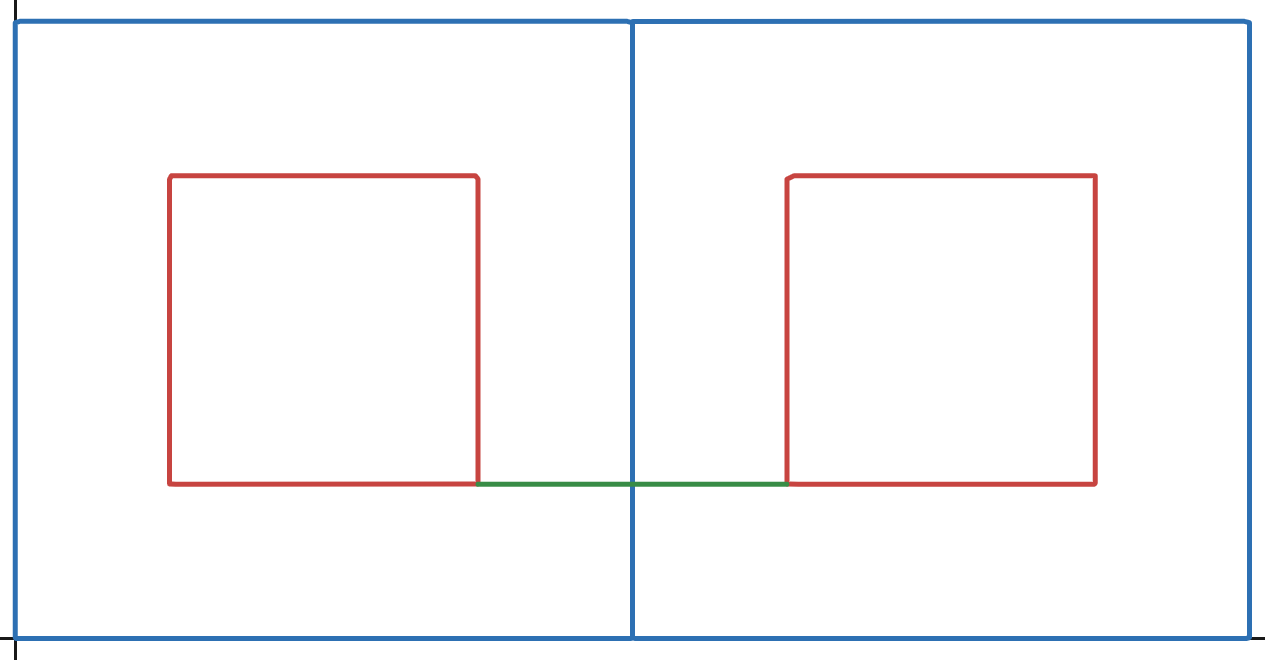
그러나 기하학을 곁들여서 생각해보면 이번에는 뢸로삼각형을 아래와 같이 나눠볼 수 있을 것 같네요!

예 색칠을 좀 해봤습니다!

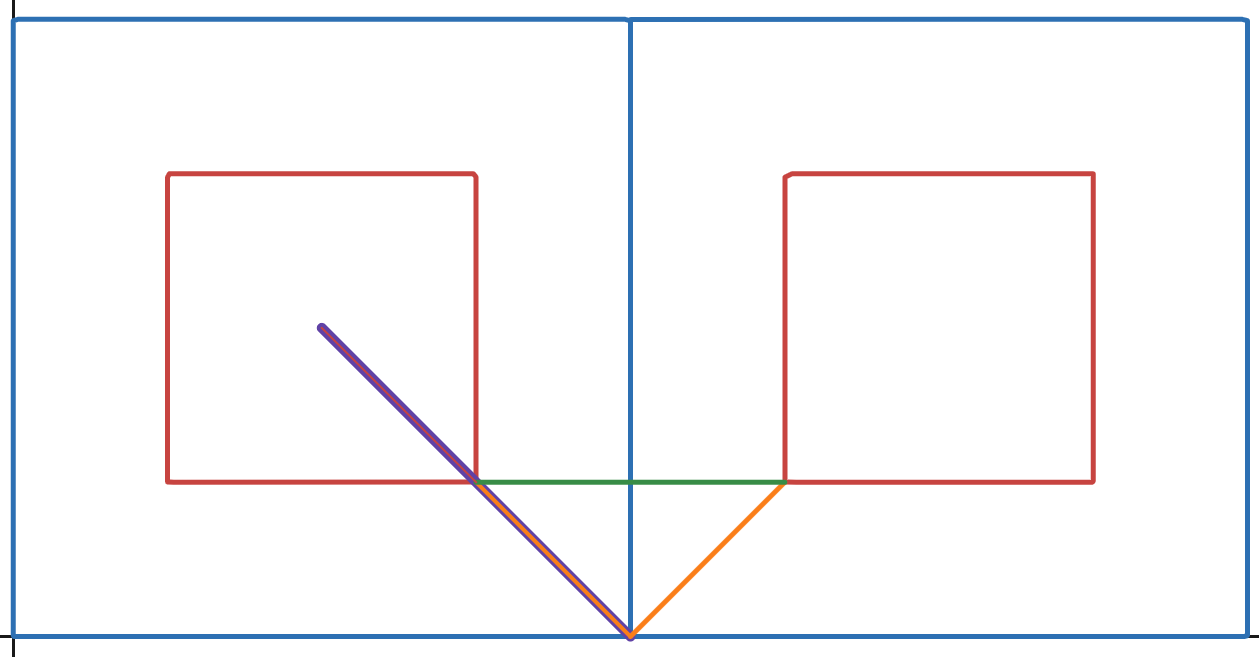
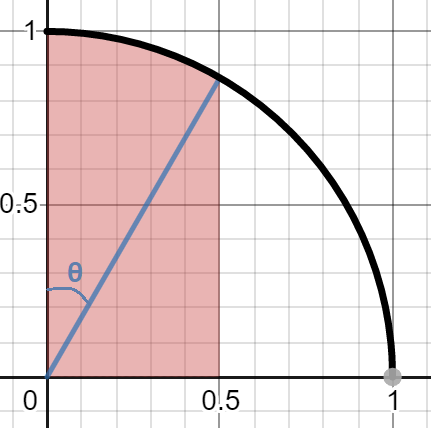
저 자주색 영역이(빗금까지 포함해서) 부채꼴입니다. 뢸로 삼각형의 정의가 한 꼭지점을 원점으로하여 다른 두 꼭지점을 연결하는 원의 일부분을 그리는 것이었으니 당연히 한 꼭지점을 원점으로하는 자주색 영역은 부채꼴이 됩니다.

다만 여기서는 임의의 각 $ \theta $만큼의 부채꼴인거죠.

자 그러면 이제 뢸로삼각형의 영역의 $ \frac{1}{4} $의 넓이를 저 도형들로 살펴보죠!

먼저 자주색 부채꼴 넓이에서 빨간색 삼각형 넓이를 빼고 파란색 삼각형 넓이를 더하고 주황색 활꼴의 절반 넓이를 더하면 뢸로 삼각형의 1/4이 되겠네요!

똑같이 뢸로삼각형의 내부 정삼각형의 밑변을 y=0에 두고, 그 높이를 a라고 칭하겠습니다.

그리고 a높이에서 x위치는 이전 포스팅과 동일하게 원의 방정식으로 놓겠습니다.

그러면,

$ 자주-빨강+파랑+주황 = \frac{1}{4} 뢸로삼각형 전체 넓이 $

으로 볼 수 있고, 이거를 좀 더 있어보이게 표현해보면 아래와 같습니다.

$ A_{Sector}-A_{SectorTriangle}+A_{UpperTriangle}+\frac{1}{2}A_{Segment} = \frac{1}{4}A_{ReuleauxTriangle} $

자, 이제 각각의 넓이를 구하러 출동해보시죠

2] 각각의 넓이 구하기

차례대로 하나씩 넓이를 구해보죠

일단 자주색 부채꼴입니다.

임의의 각 $ \theta $로 계산하면 부채꼴의 넓이는

$ A_{Sector} = \frac{1}{2}d^2\theta $

이렇게 되겠죠?

다음은 빨간 삼각형입니다.

삼각형의 넓이는 밑변*높이*절반 입니다. 여기서 밑변은 폭의 절반이지만, 높이는 일반각 $ \theta $로 정의되기때문에 밑변에 $ tan\theta $를 곱한 것으로 알 수 있죠. 따라서

$ A_{SectorTriangle} = \frac{1}{2}*\frac{1}{2}d*\frac{1}{2}dtan\theta $

이 됩니다.

파란 삼각형을 보죠

빨간 삼각형과 비슷하게 밑변*높이*절반을 가져가려하나, 밑변에 해당하는 길이가 변수 a에 의해서 계속 변화합니다. 따라서 밑변은 변수 a에 의해 길이가 결정되는데, 이 법칙을 나타낸게 원의 방정식을 정리한 함수죠. 자세한 내용은 이전 포스팅에 있으니 여기서는 빠르게 수식을 세워보도록 하겠습니다.

그리고 이 파란 삼각형에서도 높이는 밑변에 tan값을 곱한 값이 되는데, 여기서 일반각은 평행한 두 직선 사이 엇각의 관계가 되므로(정확히는 내엇각(alternate interior angle)) 똑같이 $ \theta $가 됩니다.

수식으로 세워보면

$ A_{UpperTriangle} = \frac{1}{2}*(\sqrt{d^2-a^2}-\frac{d}{2})*(\sqrt{d^2-a^2}-\frac{d}{2})tan\theta $

이 됩니다.

대망의 활꼴의 절반인 주황색이 나왔습니다. 

전체 활꼴의 넓이는 아래와 같고

$ A_{Segment} = \frac{1}{2}d^2\frac{\pi}{3}-\frac{\sqrt{3}}{4}d^2 $

이것의 절반이 주황색의 넓이죠?

전체 수식에서 나중에 1/2을 해줄테니 수식은 여기까지 세우는 걸로 하죠

마지막 뢸로 삼각형의 넓이 입니다.

$ A_{ReuleauxTriangle} = \frac{3}{2}d^2\frac{\pi}{3}-\frac{\sqrt{3}}{2}d^2 $

부채꼴넓이*3-정삼각형넓이*2 해주면 나옵니다.

이제 각각의 넓이를 다 구했으니 다 합칠까요?

아뇨... 각각만 봐도 너무 복잡한데 지금 다 합쳐버리면 길이가 너무 길어져요...

그러니 동일하게 각각 다 수식을 정리해서 마지막에 합쳐보죠!

3] 수식 정리하기

$ \frac{a}{d} = s $ 로 놓겠습니다. 그럼 $ a = ds $도 성립하겠죠?

그리고 sin함수의 정의는 임의의 각 $ \theta $에 대해 그 직각삼각형의 $ \frac{높이}{빗변} $로 정의됩니다. 따라서
$ sin\theta = \frac{a}{d} $ 가 되겠네요. 그리고 $ \frac{a}{d} = s $니까, 삼단논법으로 $ sin\theta = s $입니다.

sin을 정의했으니 다른 삼각함수들도 정의해보죠. 삼각함수들은 하나가 정해지면 다른것들로도 다 변환이 된답니다.
$ cos\theta = \sqrt{1-sin^2\theta} = \sqrt{1-s^2} $
$ tan\theta = \frac{sin\theta}{cos\theta} = \frac{s}{\sqrt{1-s^2}} $

자, 이제 간단하게 할 준비는 다 끝났습니다. 수식정리하러가죠

부채꼴은 다음과 같이 정리될겁니다. $ sin\theta=s $면 $ \theta=arcsin\ s $겠죠?

$ A_{Sector} = \frac{1}{2}d^2\theta $
$ A_{Sector} = \frac{1}{2}d^2arcsin\ s $

빨간삼각형은

$ A_{SectorTriangle} = \frac{1}{2}*\frac{1}{2}d*\frac{1}{2}dtan\theta $
$ A_{SectorTriangle} = \frac{d^2s}{8\sqrt{1-s^2}} $

파란삼각형은

$ A_{UpperTriangle} = \frac{1}{2}*(\sqrt{d^2-a^2}-\frac{d}{2})*(\sqrt{d^2-a^2}-\frac{d}{2})tan\theta $
$ A_{UpperTriangle} = \frac{d^2}{2}(\sqrt{1-s^2}-\frac{1}{2})^2\frac{s}{\sqrt{1-s^2}} $

요렇게 정리가 되겠네요!

활꼴과 뢸로 삼각형도 각각 절반, 사등분 해준 결과를 먼저 써서 정리하죠

$ \frac{1}{2}A_{Segment} = \frac{d^2}{4}(\frac{\pi}{3}-\frac{\sqrt{3}}{2}) $
$ \frac{1}{4}A_{ReuleauxTriangle} = \frac{d^2}{8}(\pi-\sqrt{3}) $

이 두개는 상수항이므로 먼저 계산을 통해 정리해보도록 하겠습니다.

$ A_{Sector}-A_{SectorTriangle}+A_{UpperTriangle}+\frac{1}{2}A_{Segment} = \frac{1}{4}A_{ReuleauxTriangle} $

이게 전체식이구요, 상수항을 이항해서

$ A_{Sector}-A_{SectorTriangle}+A_{UpperTriangle} = \frac{1}{4}A_{ReuleauxTriangle}-\frac{1}{2}A_{Segment} $

요렇게 놓은뒤에 위에서 정리한 식을 넣고 다시 정리하면

$ A_{Sector}-A_{SectorTriangle}+A_{UpperTriangle} = \frac{d^2\pi}{24} $

요렇게 상수항이 깔끔해집니다.

이제 나머지 식들을 대입해보죠

$ \frac{1}{2}d^2arcsin\ s-\frac{d^2s}{8\sqrt{1-s^2}}+\frac{d^2}{2}(\sqrt{1-s^2}-\frac{1}{2})^2\frac{s}{\sqrt{1-s^2}} = \frac{d^2\pi}{24} $

길어졌죠? 일단 공통되는 변수를 양변 나눠줘서 일단 최대한 간단하게 해봅시다.

$ \frac{d^2}{2} $로 양변 나누면(=$ \frac{2}{d^2} $로 양변 곱하면)

$ arcsin\ s-\frac{s}{4\sqrt{1-s^2}}+(\sqrt{1-s^2}-\frac{1}{2})^2\frac{s}{\sqrt{1-s^2}} = \frac{\pi}{12} $

훨씬 간단해졌죠?

그래도 루트가 있으니까 뭔가 보기 불편합니다. 더 줄여보죠. $ u = \sqrt{1-s^2} $ 이렇게 루트를 치환해보겠습니다.

$ arcsin\ s-\frac{s}{4u}+(u-\frac{1}{2})^2\frac{s}{u} = \frac{\pi}{12} $

보기 훨씬 편하죠?

이제 세번째 항의 제곱을 풀어봅시다. 아주 수식이 간단하니 그 옆에 있는 곱셈으로 연결된 부분까지 같이 곱해주죠. 이렇게 간단하게 놓은 상황에서 풀면 간단하지만, 처음부터 풀어버리려면 아주 복잡했겠죠?

$ arcsin\ s-\frac{s}{4u}+(su-s+\frac{s}{4u}) = \frac{\pi}{12} $

보면 $ \frac{s}{4u} $가 덧셈 뺄셈으로 있네요? 소거해주면

$ arcsin\ s+su-s = \frac{\pi}{12} $

와우 엄청 간단한 식이 나왔네요

이제 줄이고 줄인 식이니까, 다시 치환한 변수들을 원래 변수들로 돌려주죠.

일단 u를 다시 s로,

$ arcsin\ s+s\sqrt{1-s^2}-s = \frac{\pi}{12} $

그리고 s를 다시 a와 d로 바꿔줍니다.

$ arcsin \frac{a}{d}+\frac{a}{d}\sqrt{1-\left(\frac{a}{d}\right)^2}-\frac{a}{d} = \frac{\pi}{12} $

그러면!!

바로 적분으로 풀었던 식과 완전 동일한 식이 짜잔 하고 나타난답니다.

결론-

조금 번거롭지만 복잡한 적분 없이도 풀 수 있었던 것이었습니다!

[수학/패러독스] 아리스토텔레스의 바퀴 역설(Aristotle's wheel paradox)

말머리-

안녕하세요 여러분!

오랜만에 글감을 들고 찾아왔습니다.

오늘 소개드릴 내용은 바로 '바퀴 역설' 혹은 'Wheel paradox'라는 건데요

도대체 뭐가 '역설'일까요?

소개시켜드리겠습니다!

위 이미지가 보이시나요?

이미지에는 큰 바퀴(파란색)과 그 안에 고정된 작은 바퀴(빨간색)이 있습니다.

이 두 바퀴는 따로 떼서 굴려보면 딱 그 바퀴의 원주(원 둘레)만큼 굴러가며 딱 한바퀴를 돌 겁니다.

그! 런! 데!

이 두 바퀴를 정 가운데 딱 붙여서 굴리는 순! 간!

큰 바퀴가 한바퀴 굴러갈 때, 그 거리만큼 작은 바퀴도 딱 한바퀴 도는 일이 발생하는 것이죠!

두 바퀴가 동시에 굴러갈 때, 큰 바퀴가 굴러간 거리 만큼 작은 바퀴도 같은 거리를 이동하는 겁니다!

아니 어떻게 이런일이!?

분명 떼어 놓으면 한바퀴 도는 거리가 다른데, 붙이면 같아진다!?

그래서 이것이 바로 역설(paradox), 패러독스입니다.

참고로 기원전 학자인 아리스토텔레스(Aristotle)의 이름이 붙은 만큼 엄청 오래된 역설이라는 거죠!

[더불어 제논의 역설도 고대 그리스에서 나온 걸 보면 역시 철학의 시대가 아니었나 싶네요]

그럼 도대체 이런 문제가 발생하는 이유는 뭘까요? 원인부터 살펴봅시다.

원인-

자, 이 문제를 해결하려면 원인을 일단 잘 살펴봐야겠죠?

1) 사이클로이드로 생각해보기

자 일단 사이클로이드가 궁금하시다면 >>여기<<에서 관련 내용을 한번 살펴보시기 바랍니다.

간단하게 말해 원에서 점 하나 찍고 그 원의 궤적을 보는게 사이클로이드입니다.

그렇다면 큰원에 점을 찍고, 작은 원에 점을 찍고 그 궤적을 본다면?

요런 자취가 나올겁니다. 자취는 점선으로 나타나있어요.

잘 보면 파란 자취와 빨간 자취가 다르죠?

그러니까 뭔가 운동이 다를 거라는 걸 암시하죠

보면 파란색 점선이 위아래로 더 많이 움직이고, 빨간색 점선은 위아래로 덜 움직이는데, 결국 총 이동한 거리는 같다고 한다면 당연히 빨간색이 좀 더 '효율적'으로 움직인 거니 수평방향으로 더 많이 움직였다는 사실을 도출해 낼 수 있습니다.

그러나 뭔가 조금 찝찝하죠?

2) 다각형으로 생각해보기

원은 다른말로 '무한각형'이라고도 합니다.

실제로 삼각형>사각형>오각형>... 이런식으로 각형을 늘려나가다보면 점점 원에 가까워지는 모습을 볼 수 있는데요

그렇다면 원에서의 문제이니까 각형을 줄여봅시다!

무한에서 줄이고 줄여서~~~ 사각형으로 가보죠!

자, 이런 네모바퀴가 굴러가는걸로 생각해봅시다.

이 네모바퀴는 총 네번을 굴러 가면 한바퀴를 돌 겁니다.

근데, 자세히보면, 큰 네모는 딱 붙어서 도는데, 작은 네모는 공간이 떨어져있네요?

요 초록 선 만큼요

아... 이제 감이 올 것 같습니다.

이 안에 있는 바퀴는 공간을 점프해서 이동하는 거였군요!?

그래서 큰 바퀴가 딱 한바퀴 도는동안 같은 거리를 이동할 수 있었던 거네요!

여기서 오각형>육각형 등 각수를 계속 늘려가면 이 초록선은 점점 짧아지겠지만, 더욱 많아지겠고, 사라지지는 않겠군요!

그렇다면 원은!? 아주 미세하게 이 초록선들이 거의 점으로 분포되어 보이지 않는 걸겁니다!

아하! 해결했습니다! 너무 미세해서 보이지 않지만 있다!

그럼 원은 '점프'라기보다는 아주아주 미세하게 '미끄러진다'라고도 볼 수 있겠네요?

(그러나 실제는 너무너무 작아서 얘가 점프를 하는지 미끄러지는지는 알기 어렵겠죠?)

자, 그럼 왠지 이 길이를 구하고 싶어지지 않나요?

수식으로 한번 풀어보죠!

이 애매한 거리를 수식으로 풀어보기!-

자자, 이제 수식으로 풀어보려고 하니까 일단 한가지 생각해보죠

어떤 n각형이 한 변에서 다른 변으로 돌때 돌아가는 각도는 그 n각형의 외각과 같습니다.

가령 삼각형은 120도를 돌아가 다음 변으로 돌아가겠고, 위에서 봤듯이 사각형은 90도를 돌면 다음 변으로 돌아갑니다.

마찬가지로 오각형은 72도를 돌면 다음 변으로 돌아가겠네요!

어.. 각형이 작아질수록 다음 변까지 돌아가는 각도가 작군요!

이를 수식으로 써보면 $ \theta = \frac{360}{n} $일겁니다.

좀 더 보기 편하게 60분법 각도를 호도법(radian)으로 바꿔주면, $ \theta = \frac{2 \pi}{n} $이 되겠네요.

자 그럼 도형에 열심히 보조선을 그어봅시다!

자, 여기 보라색선은 큰 바퀴의 반지름(이 될 예정인)입니다. (이를 a라고 하죠)

빨간색 바퀴의 안에 그려진 빨간색 선 또한 작은 바퀴의 반지름일 것입니다. (이를 b라고 해보겠습니다)

그리고 주황색 선은 큰 바퀴의 반지름-작은 바퀴의 반지름이죠 ( a-b 겠네요)

왜 저 주황색 선을 만들었냐면~ 초록색 선의 길이를 알고 싶기 때문이죠!

그리고 n각형의 바퀴는 한 변만큼 돌아갈 때 $ \theta $만큼의 각도로 돌아간다고 이미 정의를 했고, 주황색 선도 마찬가지로 $ \theta $만큼 돌겠죠

자, 각도와 변이 나오면 뭘 할 수 있다? 바로 삼각함수로 다른 변을 구할 수 있다!

일단 $ \theta $와 주황색 선 만으로는 바로 초록색 선의 길이를 구할 수 없으니 뭐든지 반을 똥강내봅시다.

일단 초록색 선의 반을 구하고 싶다면, 주황색 선 * $ \theta $의 절반을 하면 될 겁니다 수식으로 써보죠

근데 자꾸 무슨색 선~하니까 좀 헛갈리네요! 다시정의하죠

초록샌 선은 결국 우리가 구하고 싶은 선이니까 x라고 합시다

주황색 선은 a-b

돌아가는 각도 = 주황색 선의 각도 = $ \theta $

자, 전체 x길의 반은 (a-b)에다가 $ \theta $ 절반의 sin값을 곱해주면 나오게 되겠네요

$ \frac{x}{2} = (a-b)sin (\frac{\theta}{2}) $

자, 근데 저희는 $ \theta $를 아까 $ \frac{2 \pi}{n} $이라고 했으니

$ \frac{x}{2} = (a-b) * sin (\frac{2\pi}{2n}) $

$ \frac{x}{2} = (a-b) * sin (\frac{\pi}{n}) $

자, 왼쪽에 자꾸 2로 나누어져 있으니까 이제 양변에 2를 곱해서 전체 x길이에 대한 수식으로 바꿔보죠

$ x = 2(a-b) * sin (\frac{\pi}{n}) $

아, 근데 우리는 초록선 '단 하나'만 구했네요? 초록선은 바퀴가 n번 돌아 한바퀴 돌때까지 n개가 생기니까...

수식 복잡하게 하지말고 다시 정리하죠 $ n*x = L $이라고 새로 정의해봅시다. 초록선 n개가 모인걸 대문자 L로 놓을께요

$ L = 2*(a-b)*sin(\frac{\pi}{n})*n $

자 이제 어떤 n각형에 대해서 작은 바퀴가 점프하는 거리를 구하는 식이 완성되었습니다.

근데 아까 원은 무슨각형이다? 무한각형!

그럼 n이? 무한대!

근데 여기서 그냥 무한대 사용하면 수식이 '아니 뭐가 뭐지?'싶어지니 정리를 조금 해봅시다!

정말 재밌는 수식이 있는데요

$ \lim\limits_{x \to \infty} \frac{sin x}{x} $

는 뭐게요?

답은 1이랍니다! 그러므로!

$ L = 2*(a-b)*sin(\frac{\pi}{n})*n \Leftrightarrow L = 2*(a-b)*sin(\frac{\pi}{n})*n*\frac{\pi}{n}*\frac{1}{\frac{\pi}{n}} $

$ L = 2*(a-b)*\frac{sin(\frac{\pi}{n})}{\frac{\pi}{n}}*n*\frac{\pi}{n} $

$ L = 2*(a-b)*\frac{sin(\frac{\pi}{n})}{\frac{\pi}{n}}*\pi $

자, 항등식을 이용한 식변형을 했구요

이제 $ \lim\limits{x \to \infty} \frac{sin x}{x} $ 요 꼴이 나왔으니 바로 극한을 걸어봅시다.

$ L = \lim\limits{x \to \infty} 2*(a-b)*\frac{sin(\frac{\pi}{n})}{\frac{\pi}{n}}*\pi $

$ L = 2*(a-b)*\pi $

$ L = 2\pi(a-b) $

원에서 가칭 '점프하는 구간'의 길이를 구했습니다!

그리고 정말 신기하게도 큰 원의 원주길이($ 2\pi a $)에서 작은 원의 원주길이($ 2\pi b $)를 뺀만큼이 점프하는 구간이라는 답이 나왔네요!

결론-

결국, 안쪽의 원은 아주 조금씩 모종의 방법으로 이동하며 큰 원이 움직이는 만큼을 따라가고 있었던 것이었습니다 여러분!!

직선 두개로 원을 삼등분하기

원을 삼등분하는 방법은 정말 여러가지가 있다.

일본에서는 챌린지까지 열릴정도라고하니 열기가 대단함을 알 수 있다.

그 중에는 실용적인 것도 있지만, 오로지 수학적 아름다움만을 위해 있는 것들도 있고... 하지만, 이번에 소개하려는 방식은 그 챌린지에 없지만, 실용적으로 쓸 수 있는 직선 두개로 원을 삼등분 하는 방식이다.

물론 수치가 완전히 딱 떨어지게는 나오지 않기 때문에 실전에서 사용하려면 어느정도 비슷한 근사치로 봐야하지만, 그래도 빠르게 직선만으로 3등분을 내기에는 적합하지 않나 싶다.

그래서 우리의 목표는

위와같이 원을 세로로 한번, 가로로 한번 잘라 면적이 동일하게 나오게 하는 것이다. 면적이 동일하면 3등분!

그렇지만, 따져보면 왼쪽의 두 부분은 위아래 대칭으로 한쪽 넓이만 계산하면 자동으로 반대편 넓이가 나오므로, 여기서 가장 중요한 포인트는 첫번째 세로로 자를 때 주황부분과 초록부분이 넓이가 같아지는지가 제일중요하게 된다.

그러면 어느 x점에서 잘라야 하는지가 중요해지고, 이것만 계산할 수 있으면 원을 직선 두개로 삼등분 할 수 있게 된다.

자, 그러면 두 넓이가 같다는 식을 세워보자

음영처리된 부분의 넓이를 구하는게 키포인트인데, 일단 간단하게 음영처리된 부분의 넓이를 $ a $라고 하고 넓이구하는 식을 만들어 봅시다. 원은 단위원으로 반지름은 1입니다.

(노란부분) $ \frac{\pi}{4} + a = 2(\frac{\pi}{4} - a) $ (초록부분)

근데 식을 써보니 식이 a에 대해서 정리될 것 같습니다.

$ \frac{\pi}{4} + a = 2(\frac{\pi}{4} - a) $

$ 3a = \frac{\pi}{4} $

$ a = \frac{\pi}{12} $

즉, 전체 넓이를 구하는 식에서 음영처리된 넓이가 $ \frac{\pi}{12} $면 된다는 식으로 식이 더 간단해 졌군요.

그럼 이제 우리는 음영처리된 넓이만 구하면 되겠습니다.

1) 각도와 삼각함수로 구하기

이전 포스팅(링크)에서 구했던 방식인데, 여기서 x값으로 다시 나타내지 않고, 각도값 그대로 사용하여 푸는 방식입니다.

원과 각도가 주어졌고, 위와 같은 모양의 넓이면, 호의 넓이+삼각형 넓이 해서 구할수 있으며, 이 식은

$ \frac{1}{2} \theta $ (호의 넓이) + $ \frac{1}{2} sin\theta \cdot cos\theta $ (삼각형의 넓이) [r=1 생략]

그러면 우리가 구하고자 했던 $ \frac{\pi}{12} $로 방정식을 놓으면

$ \frac{1}{2} \theta + \frac{1}{2} sin\theta \cdot cos\theta = \frac{\pi}{12} $

정리하면

$ \theta + sin\theta \cdot cos\theta = \frac{\pi}{6} $

가 됩니다. 전에도 말씀드렸다시피 삼각함수의 일반각 계산은 사람이 할 수 없으므로 울프람 알파(https://www.wolframalpha.com/)를 돌려줍니다.

[위 식을 그대로 긁어서 붙이면 울프람에서 인식을 못합니다. θ + sin θ ⋅ cos θ = π/6 이거를 붙여 넣어주세요]

그러면 결과가

$ \theta = 0.268133... $

으로 나옵니다.

그러나 이거는 각도 값일 뿐, 우리가 원하는 것은 x좌표이므로, 위의 그림에서 놓은 $ \theta $ 방향을 보면, $ sin \theta $가 x좌표임을 알 수 있습니다.

다시 $ sin \theta $에 0.268133값을 넣어서 울프람 알파를 돌리면

$ sin 0.268133 = 0.264932... = x $

이와 같은 값을 얻고, 이는 바로 x좌표입니다.

2) 부정적분으로 구하기

이전 포스팅(링크)에서 주야장천 구했던 식을 가지고 푸는 방법입니다.

물론 계산은 울프람 알파가 해줄겁니다.

먼저 방정식을 세웁니다.

$ \frac{1}{2} \cdot x \cdot \sqrt{1-x^{2}} + \frac{1}{2} \cdot arcsin \, x = \frac{\pi}{12} $

정리하여

$ x \cdot \sqrt{1-x^{2}} + arcsin \, x = \frac{\pi}{6} $

으로 만들고 울프람을 돌리겠습니다. 마찬가지로 위 식을 그대로 붙이면 울프람에서 인식 못하니 x ⋅ √ (1 − x^2) + arcsin x = π/6로 붙여넣어 주세요.

그러면 이번에는 한번에 x 값을 알려줍니다. 결과는 1)번과 같습니다.

결론

위의 계산으로 단위원의 원점에서 약 0.265만큼 떨어진 위치에서 세로로 한번, 나머지 부분에 가로로 한번 잘라주면 3등분이 된다는 사실을 알았네요!

좀 더 실용적으로 말해보자면 어떤 크기의 원이든, 원점에서 약 1/4 지점보다 조금 더 나가서 T자로 자르면 3분할이 된다고 볼 수 있겠습니다!

원넓이의 부정적분 구하기원넓이의 부정적분 구하기 - 1) 일반공식으로 구해보기

원넓이를 처음 배우는 것은 초등학교 때, $\pi$를 3.14 근사값으로 배우면서 공식 암기와 함께 시작한다.

이후 중학교 과정에서 수의 확장과 함께 무리수로 $\pi$를 배워 무리수가 들어간 공식으로 배우고, 고등학교에 이르러서는 적분을 통해 원의 넓이를 새삼스레 다시 구해본다.

결국 우리의 수학 교과과정은 원에 대해서 배우는 것이다 라고 말해도 과언이 아닐 정도이다.

여기서 고등학교에서 정적분으로 원의 넓이를 구할 때 기계적으로 치환, 공식대입, 정적분을 통해서 '아 그냥 그렇게 되는구나'라고 알고 넘어가는 사람들이 대다수 일 터.

이번에 뭔가 궁금증이 생겨서 다시 풀어보니, 예전엔 그냥 단순히 치환하고 공식을 대입해서 풀었던 여기에는 참 많은 이유들이 있다는 것을 알게되었다.

그리하여 부정적분을 통해서 왜 이렇게 치환하고 그것으로 어떻게 넓이를 구하는지 알아보고자 한다.

물론 원은 사분원 넓이의 네배이니까 적분으로 원넓이 공식을 유도할 때 처럼, 반지름이 1인 단위원을 기준으로 하여 사분원의 넓이를 구하는 식으로 진행한다.

1] 일반식으로 원 넓이 구하기

부정적분으로 넘어가기 전에, 우리가 아는 일반 공식으로 $x$축에 대한 원의 넓이를 구할 수 있다.

딱 위의 그림에서와 같이 한번에 구하려면 왠지 적분을 써야 할 것 같지만,

위 그림과 같이 부채꼴과 삼각형으로 나눠서 구한다면 쉽게 원의 부분 넓이를 구할 수 있다.

부채꼴의 넓이는 호도법으로 전체 각도($2\pi$(360도))에 대한 원 넓이 $\pi r^2$을 전체 각도에 대한 부분각도의 비 만큼 곱해주면( $\frac{\theta}{2\pi}$ ) 부채꼴의 넓이($\frac{\theta}{2\pi}*\pi r^2 = \frac{1}{2} r^2\theta$)가 나온다.

물론 여기서는 r(반지름)을 1로 놨으니 r 변수는 사라질 것이다.

부채꼴의 각도를 기준으로 놨으니, 이제 삼각형도 계산할 수 있다. 삼각형의 넓이는 가로*세로/2이다.

xy좌표축의 x와 y의 값을 $\theta$로 표현하면 단위원의 매개변수 표현법에 의거 $y=sin\theta, x=cos\theta$로 표현할 수 있다. 다만 여기서는 부채꼴의 각도를 기준으로 표현을 했으니 우리가 쓰는 좌표축의 $y$값이 $cos\theta$가 될것이며 $x$값은 $sin\theta$가 될 것이다. 뭔가 두 길이가 달라진 것 같지만, 사실상 직사각형에서의 삼각형이니 두개는 대칭이다.(엄밀히 매개변수 표현법으로 $y=sin\theta, x=cos\theta$이니, 위의 예에서 $y=sin(90-\theta), x=cos(90-\theta)$가 되고 각각, $y=sin(90-\theta)=cos\theta$, $x=cos(90-\theta)=sin\theta$의 관계가 성립한다.)

수식으로 표현하면 $\frac{1}{2}sin\theta cos\theta$가 삼각형의 넓이가 될 것이다.

그리하여 두 식을 더한 $\frac{1}{2} \theta + \frac{1}{2}sin\theta cos\theta$ 값이 저 사다리꼴과 같은 도형의 부분 넓이가 된다는 것을 알았다.

여기까지 우리는 각도를 알면 그 각도에 해당하는 원의 사다리꼴과 같은 도형의 부분넓이를 구할 수 있게 되었으나, 반드시 각도를 알아야 한다는 단점이 있다.

여기서 x축 값 만으로 이 넓이를 구하려면, arcsin값만 알면 된다. 위의 그래프에서 x값과 같은 값을 나타내는 것은 $\theta$ 각도를 가지고 구한 $sin$값과 같다는 것을 알 수 있다. 그렇다면, 반대로 x값을 sin함수의 역함수인 arcsin에 넣어주면, 그 값에 해당하는 각도가 구해질 것이고, 그 각도값으로 부채꼴의 넓이 공식에 적용하면 부채꼴의 넓이를 알 수 있으므로 arcsin만 써주면 해결이다.

그렇다면 삼각형 부분은 어떻게 해결할 것인가?

사실 이 삼각형 부분은 x축 값이 밑변, 원의 방정식에서 x값을 대입한 값이 y값이다. 즉, y값은 $y = \sqrt{1-x^2}$이다.

이렇게 되면, 우리는 일반식으로 원에서의 사다리꼴과 같은 형태의 넓이를 x값에 따라 얻을 수 있는 일반식을 만들 수 있다.

$\frac{1}{2} arcsin\, x + \frac{1}{2}\cdot x \cdot \sqrt{1-x^2}$

다음 포스팅에서는 이를 부정적분으로 구해보는 시간을 가져볼 예정이다.