푸리에 오디세이(Fourier Odyssey): 푸리에 해석(Fourier Analysis)
0) 서론
이로써 저번까지 푸리에 급수에 대해서 완벽하게 알아보았습니다.
그렇게 '특정 구간내에서 정의된 임의의 함수도 삼각함수로 근사할수 있지롱!'에서 끝나는 것 같았는데...
1) 푸리에.. 해석...???
이 푸리에 급수를 보던 사람들이 또 다른 생각을 반짝이기 시작합니다.
이전에 직교성에서도 알아봤듯이 직교하는 두 함수는 두개의 '축'이라고 볼 수도 있다고 했잖아요?
그리고 두개의 축이 각자 어느정도인지만 정해주면 그 공간상에서 모든 점을 표현할 수도 있다고 했습니다.
그 말인 즉슨 임의의 주기함수도 sin과 cos의 조합으로 만들 수 있다는 셈이 됩니다.
더불어 주파수가 다른 sin과 cos도 서로 직교한다고했으니, 이 개념까지 더하면
'특정 주파수를 가지는 임의의 순수 정현파(pure sinusoid wave)를 만들어낼 수 있다'가 됩니다.
여기서 정현파(sinusoid wave)는 sin, cos과 같은 물결파(단일 주파수 파형(pure single-frequency wave))를 말합니다.
그리고 이 기본 주파수의 모든 정수배를 다 더하고, 각 항에 해당하는 '푸리에 계수'를 곱해주게 되면 결과적으로 독특한 파형을 나타내게 되고, 이게 결국 특정 구간에서 임의의 함수를 근사해 내게 되죠.
여기서 관점을 조금만 바꿔보면 푸리에 급수는 이제 단순히 '임의의 함수'를 근사하는데에서 멈추지 않고, '임의의 함수'를 주파수별로 '분해'까지 할 수 있다는 걸 알게된거죠!
그리고 그 주파수별 분해는 결국 cos과 sin의 계수인 $a_n$과 $b_n$에 의해 가능해집니다.
이것을 푸리에 해석이라고 합니다.
이 강력한 관점의 전환은 세상을 바꾸어 놓았습니다.
예를 들어, 오디오 이퀄라이저(EQ)는 소리라는 복잡한 파형을 푸리에 해석으로 주파수별로 분해한 뒤, 특정 주파수(저음, 고음 등)의 진폭을 조절하고 다시 합치는 원리입니다.
MP3 압축은 사람이 잘 듣지 못하는 주파수 성분을 찾아내 진폭을 줄여 데이터 크기를 줄이는 기술이죠.
즉, 시간의 흐름 속에서는 파악하기 힘든 신호의 '특성'을 주파수 세계에서는 명확히 볼 수 있게 된 것입니다.
2) 이미지로 생각해보기
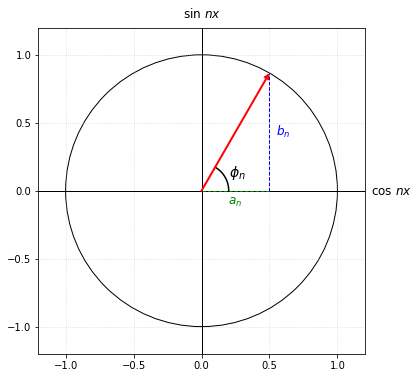
단위원에서 cos nx축과 sin nx축을 생각해봅시다.
푸리에 해석은 다음 두 가지 핵심 정보를 알려줍니다.
1] 진폭(Magnitude or Amplitude): 각 주파수 성분이 얼마나 강한가?
특정 주파수에서의 진폭은 cos 축으로 $a_n$, sin축으로 $b_n$만큼인 빨간 벡터의 길이와 같습니다.
즉, 진폭의 크기는 $\sqrt{a_n^2+b_n^2} $이죠.(피타고라스 정리죠?)
2] 위상(Phase): 각 주파수 성분이 어떤 타이밍에서 시작하는가?
또한 특정 주파수에서의 위상(=시작점)은 이 벡터의 각도와 같습니다.
즉, $\phi_n = \tan^{-1}(\frac{b_n}{a_n}) $이죠.
그리고 이걸 기본주파수의 정수배인 모든 주파수에 대하여 해석할 수 있게 된겁니다!
패러다임 시프트죠. 시간에 대한 함수를 주파수로 분해하다니요!
3) 주파수 스펙트럼
여기서 한발 더 나아가보자면, 분석의 결과를 그래프화 할 수도 있지 않을까요?
그리고 이 그림을 바로 '주파수 스펙트럼'이라고 합니다.
우리가 두가지의 정보(진폭, 위상)을 알수 있었던 만큼, 이 '주파수 스펙트럼'도 두 가지가 있는데요

1] 한가지는 가로축은 주파수, 세로축은 해당 주파수 성분의 세기(진폭)를 나타낸 주파수 스펙트럼입니다.
위의 그림에서 첫 번째 그래프죠.
이 스펙트럼을 보면, 어떤 복잡한 파형이라도 '어떤 주파수 성분들이 얼마나 강하게 섞여있는지'를 한눈에 파악할 수 있습니다. 예를 들어 사각파(Square Wave)를 주파수로 분해하면, 기본 주파수와 그 홀수배 주파수들(3배, 5배, 7배...)의 성분만 나타나는 독특한 스펙트럼을 보여줍니다.
우리가 흔히 '저음이 풍부하다' 또는 '고음이 날카롭다'라고 말할 때 주로 이 진폭 스펙트럼을 이야기하는 것입니다.
2] 다른 한가지는 가로축은 주파수, 세로축은 해당 주파수 성분의 위상을 나타낸 주파수 스펙트럼입니다.
위의 그림에서 두 번째 그래프입니다.
이 스펙트럼은 '각 주파수 성분이 어떤 타이밍(시작점)에서 시작하는가?'를 알려주면서, 파형의 실제 모양을 결정합니다. 모든 주파수 성분들이 어떻게 정렬되어 더해지는지를 지시하여, 뾰족한 부분, 완만한 부분 등 신호의 구체적인 형태를 만들어냅니다.
4) 마무리
이번에는 저번 포스팅까지 수학적으로 어려운 길을 지나신 여러분께 약간의 휴식을 드릴 겸 개념적인 내용으로 채워보았습니다.
이 포스팅에서 여러 이야기가 나왔지만, 최종적으로 정리해보자면 결국
임의의 함수를 근사하기 위해 만들어졌던 푸리에 급수가,
발상의 전환으로
임의의 함수를 푸리에 급수로 나타내었을 때 각 주파수 별로 분해할 수 있게 되었고
이를 바탕으로 임의의 함수를 주파수 별로 분석할 수 있는 툴을 제공해주었다.
입니다.
그리고 이 발상의 전환을 '푸리에 해석'이라고 하죠.
근데 여기서 조금만 더 생각해보면 이 주파수별로 분해된 정보들(진폭, 위상)을 이용해서 거꾸로 '임의의 함수'를 다시 '합성' 할 수도 있지 않을까요?
말 그대로 분해의 역과정이죠!
그래서 일반적으로 '푸리에 해석'이라고하면 그 안에 '분해'와 '합성'을 전부 포함하는 의미로 사용합니다.
그러나 가끔 푸리에 '해석'을 '분해'와 동일하게 생각하는 경우엔 '합성'을 '푸리에 역해석'이라고 부르기도 한답니다.
푸리에 오디세이는 아직 끝나지 않았고, 앞으로 다룰 내용이 많지만 급수가 끝나는 바로 이 시점에서 '푸리에 해석'을 소개시켜드린건,
사실상 '푸리에 급수'만 가지고도 '해석'이 가능하다는 걸 알려드리고 싶어서였습니다.(말 그대로 '발상의 전환' 즉, '개념'이었기 때문에 사실상 '푸리에 ~~~'인 모든 툴을 가지고 하는 '행위'가 '푸리에 해석'인거죠!)
결국 푸리에 해석이라는 개념은 '시간'축에서의 함수를 또다른 하나의 축인 '주파수'축을 추가하여 다른 관점에서 볼 수 있게 만들어준 '패러다임 시프트'였습니다!
마지막으로 이 '패러다임 시프트'를 시각적으로 이해하기 좋은 이미지를 하나 첨부하고 이번 포스팅을 마무리하겠습니다.

'Study > Mathematics' 카테고리의 다른 글
| 푸리에 오디세이(Fourier Odyssey): 푸리에 변환(Fourier Transform) (0) | 2025.11.09 |
|---|---|
| 푸리에 오디세이(Fourier Odyssey): 푸리에 적분(Fourier Integral) (0) | 2025.11.08 |
| 푸리에 오디세이(Fourier Odyssey): 푸리에 급수(Fourier Series)4 ~ 계수 (0) | 2025.11.06 |
| 푸리에 오디세이(Fourier Odyssey): 푸리에 급수(Fourier Series)3 ~ 직교성 (0) | 2025.11.05 |
| 푸리에 오디세이(Fourier Odyssey): 푸리에 급수(Fourier Series)2 ~ 근사식을 만들어 보자! (0) | 2025.11.04 |
